题目内容
16.已知函数f(x)=-x5-3x3-5x+3,若f(a)+f(a-2)>6,则实数a的取值范围是( )| A. | (-∞,3) | B. | (3,+∞) | C. | (1,+∞) | D. | (-∞,1) |
分析 由函数的解析式,算出f(-x)+f(x)=6对任意的x均成立.因此原不等式等价于f(a-2)>f(-a),再利用导数证出f(x)是R上的单调减函数,可得原不等式即a-2<-a,由此即可解出实数a的取值范围.
解答 解:∵f(x)=-x5-3x3-5x+3,
∴f(-x)=x5+3x3+5x+3,可得f(-x)+f(x)=6对任意的x均成立.
因此不等式f(a)+f(a-2)>6,即f(a-2)>6-f(a),
等价于f(a-2)>f(-a)
∵f'(x)=-5x4-9x2-5<0恒成立,
∴f(x)是R上的单调减函数,
所以由f(a-2)>f(-a)得到a-2<-a,即a<1
故选:D
点评 本题给出多项式函数,求解关于a的不等式,着重考查了利用导数研究函数的单调性、函数的奇偶性和不等式的解法等知识,属于中档题.

练习册系列答案
相关题目
6.已知随机变量ξ服从正态分布N(0,σ2),若P(ξ>3)=0.023,则P(-3≤ξ≤3)=( )
| A. | 0.954 | B. | 0.023 | C. | 0.977 | D. | 0.046 |
7.已知正项等比数列{an}满足a7=a6+2a5,若存在两项am,an,使得$\sqrt{{a_m}{a_n}}=4{a_1}$,则$\frac{1}{m}+\frac{4}{n}$的最小值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{4}{3}$ | C. | $\frac{25}{6}$ | D. | 不存在 |
4.函数y=(3-x2)ex的单调递增区间是( )
| A. | (-∞,0) | B. | (0,+∞) | C. | (-∞,-3) | D. | (-3,1) |
11.数列1,3,6,10,…的通项公式是( )
| A. | ${a_n}={n^2}-({n-1})$ | B. | ${a_n}={n^2}-1$ | C. | ${a_n}=\frac{{n({n+1})}}{2}$ | D. | ${a_n}={n^2}+1$ |
1.某一算法框图如图,输出的S值为( )
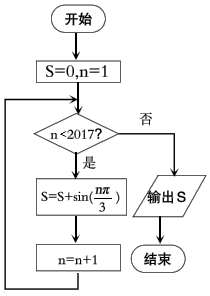

| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{3}$ | D. | 0 |
8.已知函数f(x)=m(x+m+3)(x+m+2),g(x)=2x-2,若?x∈R,f(x)<0或g(x)<0恒成立,则实数m的取值范围为( )
| A. | (-3,0) | B. | (-2,0) | C. | (-3,-2) | D. | (0,3) |
5.若函数f(x)=x2ex-a恰有三个零点,则实数a的取值范围是( )
| A. | $({\frac{4}{e^2},+∞})$ | B. | $({0,\frac{4}{e^2}})$ | C. | (0,4e2) | D. | (0,+∞) |