题目内容
16.$({{x^2}+1}){({\frac{1}{{\sqrt{x}}}-2})^5}$的展开式的常数项是( )| A. | 5 | B. | -10 | C. | -32 | D. | -42 |
分析 由于$(\frac{1}{\sqrt{x}}-2)^{5}$的通项为${C}_{5}^{r}•(\frac{1}{\sqrt{x}})^{5-r}•(-2)^{r}$,可得$({{x^2}+1}){({\frac{1}{{\sqrt{x}}}-2})^5}$的展开式的常数项.
解答 解:由于$(\frac{1}{\sqrt{x}}-2)^{5}$的通项为${C}_{5}^{r}•(\frac{1}{\sqrt{x}})^{5-r}•(-2)^{r}$,
故$({{x^2}+1}){({\frac{1}{{\sqrt{x}}}-2})^5}$的展开式的常数项是${C}_{5}^{4}•(-2)$+(-2)5=-42,
故选D.
点评 本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
相关题目
7.设复数z满足$\frac{i}{1-i}$•z=1,则|z|=( )
| A. | 1 | B. | 5 | C. | $\sqrt{2}$ | D. | 2 |
1.已知双曲线Γ:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的一条渐近线为l,圆C:(x-a)2+y2=8与l交于A,B两点,若△ABC是等腰直角三角形,且$\overrightarrow{OB}=5\overrightarrow{OA}$(其中O为坐标原点),则双曲线Γ的离心率为( )
| A. | $\frac{{2\sqrt{13}}}{3}$ | B. | $\frac{{2\sqrt{13}}}{5}$ | C. | $\frac{{\sqrt{13}}}{5}$ | D. | $\frac{{\sqrt{13}}}{3}$ |
8.已知集合A={x|y=lgx},B={x|x-1≤0},则A∩B=( )
| A. | (0,1] | B. | (0,1) | C. | (-1,1] | D. | [1,+∞) |
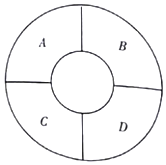 如图,一环形花坛分成A,B,C,D四块,现有3种不同的花供选种,要求在每块里种一种花,且相邻的2块种不同的花,则不同的种法总数为( )
如图,一环形花坛分成A,B,C,D四块,现有3种不同的花供选种,要求在每块里种一种花,且相邻的2块种不同的花,则不同的种法总数为( )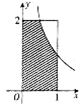 如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数$y=\frac{1}{x}(x>0)$图象下方的阴影部分区域,则阴影部分E的面积为1+ln2.
如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数$y=\frac{1}{x}(x>0)$图象下方的阴影部分区域,则阴影部分E的面积为1+ln2.