题目内容
7．设复数z满足$\frac{i}{1-i}$•z=1，则|z|=（ ）| A． | 1 | B． | 5 | C． | $\sqrt{2}$ | D． | 2 |
分析 利用两个复数代数形式的乘除法，虚数单位i的幂运算性质，把复数化简到最简形式，利用复数的模的定义求出|z|．
解答 解：复数z满足$\frac{i}{1-i}$•z=1，
∴z=$\frac{1-i}{i}$=$\frac{（1-i）i}{{i}^{2}}$=-1-i，
∴|z|=$\sqrt{（-1）^{2}+（-1）^{2}}$=$\sqrt{2}$，
故选：C
点评 本题考查两个复数代数形式的乘除法，虚数单位i的幂运算性质，复数的模的定义和求法．
练习册系列答案
相关题目
15．“大众创业，万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号．某生产企业积极响应号召，大力研发新产品，为了对新研发的一批产品进行合理定价，将该产品按事先拟定的价格进行试销，得到一组销售数据（xi，yi）（i=1，2，…，6），如表所示：
已知$\overline{y}$=$\frac{1}{6}$$\sum_{i=1}^{6}{y}_{i}$=80
（Ⅰ）求出q的值；
（Ⅱ）已知变量x，y具有线性相关关系，求产品销量y（件）关于试销单价x（元）的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\overrightarrow{a}$
（Ⅲ）用$\stackrel{∧}{{y}_{i}}$表示用正确的线性回归方程得到的与xi对应的产品销量的估计值．当销售数据（xi，yi）的残差的绝对值|$\stackrel{∧}{{y}_{i}}$-yi|≤1时，则将销售数据（xi，yi）称为一个“好数据”．现从6个销售数据中任取2个，求抽取的2个销售数据中至少有一个是“好数据”的概率．
| 试销单价x（元） | 4 | 5 | 6 | 7 | 8 | 9 |
| 产品销量y（件） | q | 84 | 83 | 80 | 75 | 68 |
（Ⅰ）求出q的值；
（Ⅱ）已知变量x，y具有线性相关关系，求产品销量y（件）关于试销单价x（元）的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\overrightarrow{a}$
（Ⅲ）用$\stackrel{∧}{{y}_{i}}$表示用正确的线性回归方程得到的与xi对应的产品销量的估计值．当销售数据（xi，yi）的残差的绝对值|$\stackrel{∧}{{y}_{i}}$-yi|≤1时，则将销售数据（xi，yi）称为一个“好数据”．现从6个销售数据中任取2个，求抽取的2个销售数据中至少有一个是“好数据”的概率．
12．已知f（x）是定义在R上的可导函数，且满足（x+1）f（x）+xf'（x）＞0，则（ ）
| A． | f（x）＞0 | B． | f（x）＜0 | C． | f（x）为减函数 | D． | f（x）为增函数 |
19．
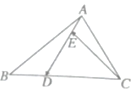如图，在△ABC中，点D在BC边上，且CD=2DB，点E在AD边上，且AD=3AE，则用向量$\overrightarrow{AB}，\overrightarrow{AC}$表示$\overrightarrow{CE}$为（ ）
如图，在△ABC中，点D在BC边上，且CD=2DB，点E在AD边上，且AD=3AE，则用向量$\overrightarrow{AB}，\overrightarrow{AC}$表示$\overrightarrow{CE}$为（ ）| A． | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}+\frac{8}{9}\overrightarrow{AC}$ | B． | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}-\frac{8}{9}\overrightarrow{AC}$ | C． | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}+\frac{7}{9}\overrightarrow{AC}$ | D． | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}-\frac{7}{9}\overrightarrow{AC}$ |
16．$（{{x^2}+1}）{（{\frac{1}{{\sqrt{x}}}-2}）^5}$的展开式的常数项是（ ）
| A． | 5 | B． | -10 | C． | -32 | D． | -42 |