题目内容
6.已知三棱锥S-ABC的三条侧棱相等,体积为$\frac{\sqrt{3}}{4}$,AB=BC=$\sqrt{3}$,∠ACB=30°,则三棱锥S-ABC外接球的体积为$\frac{32}{3}$π.分析 设定点S在底面的投影为G,因为三棱锥S-ABC的三条侧棱相等,所以GA=GB=GC=r.三棱锥S-ABC的体积V=$\frac{1}{3}×{s}_{△ABC}×SO=\frac{\sqrt{3}}{4}$,解得SO=1,三棱锥S-ABC外接球球心O在SO上.
解答 解:如图设定点S在底面的投影为G,因为三棱锥S-ABC的三条侧棱相等,所以GA=GB=GC=r.
因为AB=BC=$\sqrt{3}$,∠ACB=30°,则△ABC的外接圆半径r,2r=$\frac{AB}{sin3{0}^{0}}=2\sqrt{3}$,
三棱锥S-ABC的体积V=$\frac{1}{3}{s}_{△ABC}×SG=\frac{\sqrt{3}}{4}$,解得SG=1
三棱锥S-ABC外接球球心为O.三棱锥S-ABC外接球半径R,则R2=(SG-R)2+($\sqrt{3}$)2,
解得R=2
棱锥S-ABC外接球的体积为$\frac{4}{3}π{R}^{3}=\frac{32}{3}π$.
故答案为:$\frac{32π}{3}$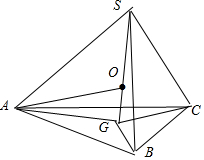
点评 本题考查了几何体的外接球,转化思想是解题关键,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.$({{x^2}+1}){({\frac{1}{{\sqrt{x}}}-2})^5}$的展开式的常数项是( )
| A. | 5 | B. | -10 | C. | -32 | D. | -42 |
11.动点P在抛物线y=2x2+1上移动,若P与点Q(0,-1)连线的中点为M,则动点M的轨迹方程为( )
| A. | y=2x2 | B. | y=4x2 | C. | y=6x2 | D. | y=8x2 |