题目内容
11．
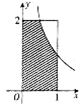如图，设D是图中边长分别为1和2的矩形区域，E是D内位于函数$y=\frac{1}{x}（x＞0）$图象下方的阴影部分区域，则阴影部分E的面积为1+ln2．
分析 首先利用定积分表示阴影部分的面积，然后计算定积分．
解答 解：由已知得到矩形面积SD=1×2=2，${S_E}=\frac{1}{2}×2+\int_{\frac{1}{2}}^1{\frac{1}{x}}dx$
=1+lnx|${\;}_{\frac{1}{2}}^{1}$=$1+ln1-ln\frac{1}{2}$=1+ln2；
故答案为：1+ln2．
点评 本题考查了利用定积分求曲边梯形的面积；关键是正确利用定积分表示面积，然后正确计算．
练习册系列答案
相关题目
19．
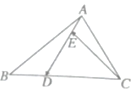如图，在△ABC中，点D在BC边上，且CD=2DB，点E在AD边上，且AD=3AE，则用向量$\overrightarrow{AB}，\overrightarrow{AC}$表示$\overrightarrow{CE}$为（ ）
如图，在△ABC中，点D在BC边上，且CD=2DB，点E在AD边上，且AD=3AE，则用向量$\overrightarrow{AB}，\overrightarrow{AC}$表示$\overrightarrow{CE}$为（ ）| A． | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}+\frac{8}{9}\overrightarrow{AC}$ | B． | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}-\frac{8}{9}\overrightarrow{AC}$ | C． | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}+\frac{7}{9}\overrightarrow{AC}$ | D． | $\overrightarrow{CE}=\frac{2}{9}\overrightarrow{AB}-\frac{7}{9}\overrightarrow{AC}$ |
16．$（{{x^2}+1}）{（{\frac{1}{{\sqrt{x}}}-2}）^5}$的展开式的常数项是（ ）
| A． | 5 | B． | -10 | C． | -32 | D． | -42 |