题目内容
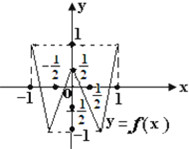 已知函数y=f(x)的定义域和值域都是[-1,1](其图象如图所示),函数g(x)=sinx,x∈[-π,π].定义:当f(x1)=0(x1∈[-1,1])且g(x2)=x1(x2∈[-π,π])时,称x2是方程f(g(x))=0的一个实数根.则方程f(g(x))=0的所有不同实数根的个数是( )
已知函数y=f(x)的定义域和值域都是[-1,1](其图象如图所示),函数g(x)=sinx,x∈[-π,π].定义:当f(x1)=0(x1∈[-1,1])且g(x2)=x1(x2∈[-π,π])时,称x2是方程f(g(x))=0的一个实数根.则方程f(g(x))=0的所有不同实数根的个数是( )| A、2 | B、4 | C、6 | D、8 |
考点:根的存在性及根的个数判断,函数的零点与方程根的关系
专题:函数的性质及应用
分析:通过图象可知方程f(x)=0数有4个非零实数解,由g(x)=sinx,x∈[-π,π],当f(x1)=0(x1∈[-1,1])且g(x2)=x1(x2∈[-π,π]),即f[g(x)]=0根的个数推出正确结论.
解答:
解:当f(x1)=0(x1∈[-1,1])且g(x2)=x1,即f[g(x)]=0
通过图象可知方程f(x)=0有4个非零实数解,分别设为t1,t2,t3,t4,
由已知中的图象可知:t1,t2,t3,t4∈(-1,1)
又∵函数g(x)=sinx,x∈[-π,π],
∴g(x)∈[-1,1],
∴g(x)分别为t1,t2,t3,t4时都有两个x值与之对应,
因此方程f(g(x))=0的所有不同实数根的个数是8个,
故选:D
通过图象可知方程f(x)=0有4个非零实数解,分别设为t1,t2,t3,t4,
由已知中的图象可知:t1,t2,t3,t4∈(-1,1)
又∵函数g(x)=sinx,x∈[-π,π],
∴g(x)∈[-1,1],
∴g(x)分别为t1,t2,t3,t4时都有两个x值与之对应,
因此方程f(g(x))=0的所有不同实数根的个数是8个,
故选:D
点评:本题考查根的存在性及根的个数判断,函数的图象,考查逻辑思维能力,是中档题.

练习册系列答案
相关题目
若抛物线y2=ax的焦点与椭圆
+
=1的左焦点重合,则a的值为( )
| x2 |
| 6 |
| y2 |
| 2 |
| A、-8 | B、-16 | C、-4 | D、4 |
已知A、B、C是直线l上不同的三个点,点O不在直线l上,则使等式x2
+x
+
=
成立的实数x的取值集合为( )
| OA |
| OB |
| BC |
| 0 |
| A、{-1} | B、∅ |
| C、{0} | D、{0,-1} |
在空间直坐标系中,点P在x轴上,它到P1(0,
,3)的距离为2
,则点P的坐标为( )
| 2 |
| 3 |
| A、(0,1,0)或(0,-1,0) |
| B、(1,0,0) |
| C、(1,0,0)或(-1,0,0) |
| D、(0,1,0)或(0,0,1) |
设r>0,那么直线xcosθ+ysinθ=r(θ是常数)与圆
(φ是参数)的位置关系是( )
|
| A、相交 | B、相切 |
| C、相离 | D、视r的大小而定 |
“sinA=
”是“A=45°”的( )
| ||
| 2 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
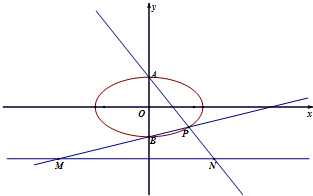 已知椭圆C:
已知椭圆C: