题目内容
已知函数g(x)=x2-(2a+1)x+alnx
(Ⅰ) 当a=1时,求函数g(x)的单调增区间;
(Ⅱ) 求函数g(x)在区间[1,e]上的最小值;
(Ⅲ) 在(Ⅰ)的条件下,设f(x)=g(x)+4x-x2-2lnx,
证明:
>
(n≥2).(参考数据:ln2≈0.6931)
(Ⅰ) 当a=1时,求函数g(x)的单调增区间;
(Ⅱ) 求函数g(x)在区间[1,e]上的最小值;
(Ⅲ) 在(Ⅰ)的条件下,设f(x)=g(x)+4x-x2-2lnx,
证明:
| n |
 |
| k=2 |
| 1 |
| k-f(k) |
| 3n2-n-2 |
| n(n+1) |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性,不等式的证明
专题:导数的综合应用
分析:(Ⅰ)由g′(x)=
>0,能求出函数f(x)的单调增区间.
(Ⅱ)g′(x)=2x-(2a+1)+
=
=0,由此根据a的取值范围分类讨论,能求出g(x)min.
(Ⅲ)证明:令h(x)=lnx-
(x2-1),由x∈[2,+∞),得h′(x)=
<0,从而得到
>2(
-
),k-f(k)=lnk,由此能证明
>
(n≥2).
| 2x2-3x+1 |
| x |
(Ⅱ)g′(x)=2x-(2a+1)+
| a |
| x |
| (2x-1)(x-a) |
| x |
(Ⅲ)证明:令h(x)=lnx-
| 1 |
| 4 |
| 2-x2 |
| 2x |
| 1 |
| lnx |
| 1 |
| x-1 |
| 1 |
| x+1 |
| n |
 |
| k=2 |
| 1 |
| k-f(k) |
| 3n2-n-2 |
| n(n+1) |
解答:
(Ⅰ)解:当a=1时,g(x)=x2-3x+lnx,
∴g′(x)=
>0,
解得x>1或x<
.
∴函数f(x)的单调增区间为(0,
),(1,+∞).
(Ⅱ)解:g(x)=x2-(2a+1)x+alnx,
g′(x)=2x-(2a+1)+
=
=
=0,
当a≤1,x∈[1,e],g′(x)>0,g(x)单调增.g(x)min=-2a,
当1<a<e,x∈(1,a),g′(x)<0,g(x)单调减.
x∈(a,e),g′(x)>0,g(x)单调增.
g(x)min=g(a)=-a2-a+alna,
当a≥e,x∈[1,e],g′(x)≤0,g(x)单调减,
g(x)min=e2-(2a+1)e+a.
∴g(x)min=
.
(Ⅲ)证明:令h(x)=lnx-
(x2-1),
∵x∈[2,+∞),h′(x)=
<0,
∴h(x)≤h(2)=ln2-
<0,即lnx<
(x2-1),
∴
>
=2(
-
),
k-f(k)=lnk,
=
=
+
+…+
>2(1-
+
-
+…+
-
+
-
)
>2(1+
-
-
)
=
,(n≥2).
∴
>
(n≥2).
∴g′(x)=
| 2x2-3x+1 |
| x |
解得x>1或x<
| 1 |
| 2 |
∴函数f(x)的单调增区间为(0,
| 1 |
| 2 |
(Ⅱ)解:g(x)=x2-(2a+1)x+alnx,
g′(x)=2x-(2a+1)+
| a |
| x |
=
| 2x2-(2a+1)x+a |
| x |
=
| (2x-1)(x-a) |
| x |
当a≤1,x∈[1,e],g′(x)>0,g(x)单调增.g(x)min=-2a,
当1<a<e,x∈(1,a),g′(x)<0,g(x)单调减.
x∈(a,e),g′(x)>0,g(x)单调增.
g(x)min=g(a)=-a2-a+alna,
当a≥e,x∈[1,e],g′(x)≤0,g(x)单调减,
g(x)min=e2-(2a+1)e+a.
∴g(x)min=
|
(Ⅲ)证明:令h(x)=lnx-
| 1 |
| 4 |
∵x∈[2,+∞),h′(x)=
| 2-x2 |
| 2x |
∴h(x)≤h(2)=ln2-
| 3 |
| 4 |
| 1 |
| 4 |
∴
| 1 |
| lnx |
| 4 |
| (x-1)(x+1) |
| 1 |
| x-1 |
| 1 |
| x+1 |
k-f(k)=lnk,
| n |
 |
| k=2 |
| 1 |
| k-f(k) |
| n |
 |
| k=2 |
| 1 |
| lnk |
| 1 |
| ln2 |
| 1 |
| ln3 |
| 1 |
| lnn |
>2(1-
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| n-2 |
| 1 |
| n |
| 1 |
| n-1 |
| 1 |
| n+1 |
>2(1+
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
=
| 3n2-n-2 |
| n(n+1) |
∴
| n |
 |
| k=2 |
| 1 |
| k-f(k) |
| 3n2-n-2 |
| n(n+1) |
点评:本题考查函数的增区间的求法,考查函数的最小值的求法,考查不等式的证明,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
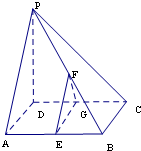 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F、G分别是AB,PB,CD的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F、G分别是AB,PB,CD的中点. 如图,在四棱锥V-ABCD中,底面ABCD为正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
如图,在四棱锥V-ABCD中,底面ABCD为正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.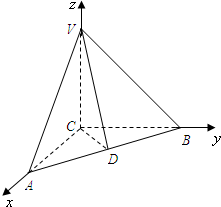 如图,在三棱锥V-ABC中,顶点C在空间直角坐标系的原点处,顶点A、B、V分别在x、y、z轴上,D是AB的中点,且AC=BC=2,∠VDC=θ.
如图,在三棱锥V-ABC中,顶点C在空间直角坐标系的原点处,顶点A、B、V分别在x、y、z轴上,D是AB的中点,且AC=BC=2,∠VDC=θ.