题目内容
19.已知向量$\overrightarrow{AB}$=(1,$\sqrt{3}$),$\overrightarrow{AC}$=(-1,$\sqrt{3}$),则∠BAC=( )| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
分析 方法一:判断△ABC为等边三角形,问题得以解决,
方法二:根据向量的夹角公式计算即可
解答 解:方法一:∵$\overrightarrow{AB}$=(1,$\sqrt{3}$),$\overrightarrow{AC}$=(-1,$\sqrt{3}$),
∴|$\overrightarrow{AB}$|=2,|$\overrightarrow{AC}$|=2,$\overrightarrow{BC}$=$\overrightarrow{AC}$-$\overrightarrow{AB}$=(-2,0),
∴|$\overrightarrow{BC}$|=2,
∴△ABC为等边三角形,
∴∠BAC=60°,
方法二::∵$\overrightarrow{AB}$=(1,$\sqrt{3}$),$\overrightarrow{AC}$=(-1,$\sqrt{3}$),
∴|$\overrightarrow{AB}$|=2,|$\overrightarrow{AC}$|=2,$\overrightarrow{AC}$•$\overrightarrow{AB}$=1×(-1)+$\sqrt{3}$×$\sqrt{3}$=2,
∴cos∠BAC=$\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AB|}•|\overrightarrow{AC}|}$=$\frac{1}{2}$,
∵0°≤∠BAC≤180°,
∴∠BAC=60°,
故选:C.
点评 本题考查了向量的夹角公式和向量的坐标运算,属于基础题

练习册系列答案
相关题目
7.由于研究性学习的需要,中学生李华持续收集了手机“微信运动”团队中特定20名成员每天行走的步数,其中某一天的数据记录如下:
5860 6520 7326 6798 7325
8430 8215 7453 7446 6754
7638 6834 6460 6830 9860
8753 9450 9860 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表(设步数为x)
(Ⅰ)写出m,n的值,若该“微信运动”团队共有120人,请估计该团队中一天行走步数不少于7500步的人数;
(Ⅱ)记C组步数数据的平均数与方差分别为v1,$s_1^2$,E组步数数据的平均数与方差分别为v2,$s_2^2$,试分别比较v1与v2,$s_1^2$与$s_2^2$的大小;(只需写出结论)
(Ⅲ)从上述A,E两个组别的步数数据中任取2个数据,求这2个数据步数差的绝对值大于3000步的概率.
5860 6520 7326 6798 7325
8430 8215 7453 7446 6754
7638 6834 6460 6830 9860
8753 9450 9860 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表(设步数为x)
| 组别 | 步数分组 | 频数 |
| A | 5500≤x<6500 | 2 |
| B | 6500≤x<7500 | 10 |
| C | 7500≤x<8500 | m |
| D | 8500≤x<9500 | 2 |
| E | 9500≤x<10500 | n |
(Ⅱ)记C组步数数据的平均数与方差分别为v1,$s_1^2$,E组步数数据的平均数与方差分别为v2,$s_2^2$,试分别比较v1与v2,$s_1^2$与$s_2^2$的大小;(只需写出结论)
(Ⅲ)从上述A,E两个组别的步数数据中任取2个数据,求这2个数据步数差的绝对值大于3000步的概率.
11.下列函数中为奇函数的是( )
| A. | y=x2+2x | B. | y=ln|x| | C. | y=($\frac{1}{3}$)x | D. | y=xcosx |
8.设0<a<1,且m=loga(a2+1),n=loga(a+1),p=loga(2a),则m,n,p的大小关系为( )
| A. | n>m>p | B. | p>m>n | C. | m>n>p | D. | m>p>n |
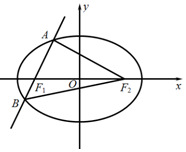 如图,已知F1、F2是椭圆G:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,直线l:y=k(x+1)经过左焦点F1,且与椭圆G交于A、B两点,△ABF2的周长为$4\sqrt{3}$.
如图,已知F1、F2是椭圆G:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,直线l:y=k(x+1)经过左焦点F1,且与椭圆G交于A、B两点,△ABF2的周长为$4\sqrt{3}$.