题目内容
4.已知{an}为等差数列,Sn为其前n项和,若a2=4,S8=-8,则a10=-12.分析 由已知条件,利用等差数列的通项公式和前n项和公式,建立方程组,求出首项和公差,由此能求出结果.
解答 解:等差数列{an}的前n项和为Sn,
∵a2=4,S8=-8,设公差为d,
∴$\left\{\begin{array}{l}{{a}_{1}+d=4}\\{8{a}_{1}+\frac{8×(8-1)d}{2}=-8}\end{array}\right.$,
解得a1=6,d=-2,
∴a10=6+9×(-2)=-12.
故答案为:-12
点评 本题考查等差数列中第10项的求法,是基础题,解题时要认真审题,要熟练掌握等差数列的性质.

练习册系列答案
相关题目
14.$\sum_{k=0}^m{C_{n-k}^{n-m}}C_n^k$=( )
| A. | 2m+n | B. | $\frac{C_n^m}{2^m}$ | C. | ${2^n}C_n^m$ | D. | ${2^m}C_n^m$ |
15.设全集U=Z,集合A={x∈Z|x(x-2)≥3},则∁UA=( )
| A. | {0,1,2,3} | B. | {-1,0,1,2} | C. | {-1,0,1,2,3} | D. | {0,1,2} |
19.已知向量$\overrightarrow{AB}$=(1,$\sqrt{3}$),$\overrightarrow{AC}$=(-1,$\sqrt{3}$),则∠BAC=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
13.在如图所示的计算1+5+9+…+2013的程序框图中,判断框内应填入( )
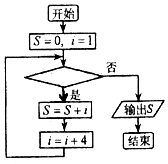

| A. | i≤504 | B. | i≤2009 | C. | i≤2013 | D. | i<2013 |
9.已知复数z满足(z-1)i=i+1,则z在复平面内所对应的点在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |