题目内容
18.己知函数f(x)=2sin2($\frac{π}{4}$+x)-$\sqrt{3}$cos2x.x∈[$\frac{π}{4}$,$\frac{π}{2}$].(1)求函数f(x)的单调区间和最值;
(2)若不等式|f(x)-m|<2在x∈[$\frac{π}{4}$,$\frac{π}{2}$]上恒成立,求实数m的取值范围.
分析 (1)首先对三角函数的关系式进行恒等变换,把函数关系式变形成正弦型函数,进一步利用正弦型函数的整体思想求出函数的单调区间和最值;
(2)首先根据函数的定义域求出函数的值域,进一步利用函数的恒成立问题求出参数的取值范围.
解答 解:(1)(x)=2sin2(x+$\frac{π}{4}$)-$\sqrt{3}$cos2x
=2(sin2x•$\frac{1}{2}$-cos2x•$\frac{\sqrt{3}}{2}$)+1
=2sin(2x-$\frac{π}{3}$)+1
所以:f(x)=2sin(2x-$\frac{π}{3}$)+1,
由x∈[$\frac{π}{4}$,$\frac{π}{2}$],可得:$\frac{π}{6}$≤2x-$\frac{π}{3}$≤$\frac{2π}{3}$,
所以由$\frac{π}{6}$≤2x-$\frac{π}{3}$≤$\frac{π}{2}$,可得递增区间为[$\frac{π}{4}$,$\frac{5π}{12}$];
由$\frac{π}{2}$≤2x-$\frac{π}{3}$≤$\frac{2π}{3}$,可得递减区间为[$\frac{5π}{12}$,$\frac{π}{2}$];
所以,函数f(x)的最大值为3,最小值为2;
(2)由(1)可得:在x∈[$\frac{π}{4}$,$\frac{π}{2}$]上函数f(x)的最大值为3,最小值为2;
使得|f(x)-m|<2在x∈[$\frac{π}{4}$,$\frac{π}{2}$]上恒成立,
即:-2<f(x)-m<2,
只需满足f(x)max-2<m<f(x)min+2即可,
可得:1<m<4.
点评 本题考查的知识要点:三角函数的恒等变换,利用函数的整体思想求出函数的单调区间,恒成立问题的应用,属于中档题.

 口算题天天练系列答案
口算题天天练系列答案| A. | $\frac{1}{2}$,π | B. | 1,π | C. | $\frac{1}{2}$,$\frac{π}{2}$ | D. | 1,$\frac{π}{2}$ |
| A. | (1,0) | B. | (0,1) | C. | (0,-1) | D. | (-1,0) |
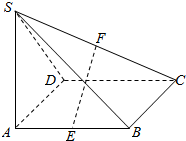 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD是正方形,且SA=AB=2.
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD是正方形,且SA=AB=2.