题目内容
已知函数f(x)=
,满足f(x)>0的x的取值范围是 .
|
考点:指、对数不等式的解法
专题:函数的性质及应用
分析:对字母x分类讨论,分别得出f(x)的式子,解不等式求出x的范围.
解答:
解:当x≤0时,f(x)=x2-2x-3
∴x2-2x-3>0
解得x<-1
当x>0时,f(x)=-1+log4x
∴-1+log4x>0
解得x>4
总之,(-∞,-1)∪(4,+∞)
故答案为:(-∞,-1)∪(4,+∞)
∴x2-2x-3>0
解得x<-1
当x>0时,f(x)=-1+log4x
∴-1+log4x>0
解得x>4
总之,(-∞,-1)∪(4,+∞)
故答案为:(-∞,-1)∪(4,+∞)
点评:本题考查分段函数的求值问题及对数不等式、二次不等式的解法,属于基础题.

练习册系列答案
相关题目
在△ABC中,a=x,b=2,B=45°,若该三角形有两个解,则x的取值范围是( )
| A、x>2 | ||
| B、x<2 | ||
C、2
| ||
D、2
|
已知椭圆的标准方程为
+
=1,则焦点坐标为( )
| x2 |
| 5 |
| y2 |
| 9 |
| A、(±2,0) |
| B、(±4,0) |
| C、(0,±4) |
| D、(0,±2) |
已知sin(3π-θ)=-2sin(
+θ),则tan2θ等于( )
| π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
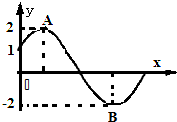 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤