题目内容
在平面直角坐标系xOy中，已知△ABC的顶点A（-5，0）和C（5，0），顶点B在双曲线
-
=1，则
的值为（ ）
| x2 |
| 16 |
| y2 |
| 9 |
| sinB |
| 丨sinA-sinC丨 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：根据双曲线的定义，以及正弦定理，即可得到结论．
解答：
解：∵在双曲线
-
=1，
∴a=4，b=3，c=5，
即A，C是双曲线的两个焦点，
∵顶点B在双曲线
-
=1，
∴|BA-BC|=2a=8，AC=10，
则由正弦定理得
=
=
=
，
故选：C．
| x2 |
| 16 |
| y2 |
| 9 |
∴a=4，b=3，c=5，
即A，C是双曲线的两个焦点，
∵顶点B在双曲线
| x2 |
| 16 |
| y2 |
| 9 |
∴|BA-BC|=2a=8，AC=10，
则由正弦定理得
| sinB |
| 丨sinA-sinC丨 |
| AC |
| |BA-BC| |
| 10 |
| 8 |
| 5 |
| 4 |
故选：C．
点评：本题主要考查双曲线的定义的应用，利用正弦定理将条件转化是解决本题的关键．
练习册系列答案
相关题目
平面向量
=（1，2），
=（4，2），
=m
+
（m∈R），且
与
的夹角等于
与
的夹角，则m=（ ）
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| c |
| b |
| A、-2 | B、-1 | C、1 | D、2 |
根据如下样本数据，得到回归方程
=bx+a，则（ ）
 |
| y |
| x | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 4.0 | 2.5 | -0.5 | 0.5 | -2.0 | -3.0 |
| A、a＞0，b＞0 |
| B、a＞0，b＜0 |
| C、a＜0，b＞0 |
| D、a＜0，b＜0 |
i为虚数单位，（
）2=（ ）
| 1-i |
| 1+i |
| A、-1 | B、1 | C、-i | D、i |
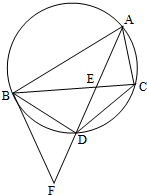如图，△ABC是圆的内接三角形，∠BAC的平分线交圆于点D，交BC于E，过点B的圆的切线与AD的延长线交于点F，在上述条件下，给出下列四个结论：①BD平分∠CBF；
②FB2=FD•FA；
③AE•CE=BE•DE；
④AF•BD=AB•BF．
所有正确结论的序号是（ ）
| A、①② | B、③④ |
| C、①②③ | D、①②④ |
设m、n是两条不同的直线，α，β是两个不同的平面，则（ ）
| A、若m⊥n，n∥α，则m⊥α |
| B、若m∥β，β⊥α，则m⊥α |
| C、若m⊥β，n⊥β，n⊥α，则m⊥α |
| D、若m⊥n，n⊥β，β⊥α，则m⊥α |
