题目内容
已知函数f(x)=x2,g(x)=2elnx(x>0)(e为自然对数的底数).
(1)求F(x)=f(x)-g(x)(x>0)的单调区间及最小值;
(2)是否存在一次函数y=kx+b(k,b∈R),使得f(x)≥kx+b且g(x)≤kx+b对一切x>0恒成立?若存在,求出该一次函数的表达式;若不存在,请说明理由.
(1)求F(x)=f(x)-g(x)(x>0)的单调区间及最小值;
(2)是否存在一次函数y=kx+b(k,b∈R),使得f(x)≥kx+b且g(x)≤kx+b对一切x>0恒成立?若存在,求出该一次函数的表达式;若不存在,请说明理由.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:存在型,导数的综合应用
分析:(1)利用导数的正负性求函数的单调区间和最最值;
(2)由函数的图象分析,如果存在一次函数,应该是两曲线的一条公共切线,先提出假设,再给出证明.
(2)由函数的图象分析,如果存在一次函数,应该是两曲线的一条公共切线,先提出假设,再给出证明.
解答:
解:(1)F′(x)=x2-2elnx
∴F′(x)=2(x-
)=
(x>0),
令F′(x)=0,得x=
(x=-
舍),
∴当0<x<
时,F′(x)<0,F(x)在(0,
)上单调递减;
当x>
时,F′(x)>0,F(x)在(
,+∞)上单调递增.
∴当x=
时,F(x)有极小值,也是最小值,
即F(x)min=F(
)=e-2eln
=0.
∴F(x)的单调递增区间为(
,+∞),单调递减区间为(0,
),最小值为0.
(2)由(1)知,f(x)与g(x)的图象有且仅有一个公共点(
,e),
∴猜想:一次函数的图象就是f(x)与g(x)的图象在点(
,e)处的公切线,
其方程为y=2
x-e.
下面证明:当x>0时,f(x)≥2
x-e,且g(x)≤2
x-e恒成立.
∵f(x)-(2
x-e)=(x-
)2≥0,∴f(x)≥2
x-e对x>0恒成立.
又令G(x)=2
x-e-g(x)=2
x-e-2eln x,∴G′(x)=2
-
=
,
∴当0<x<
时,G′(x)<0,G(x)在(0,
)上单调递减;
当x>
时,G′(x)>0,G(x)在(
,+∞)上单调递增.
∴当x=
时,G(x)有极小值,也是最小值,
即G(x)min=G(
)=2e-e-2eln
=0,∴G(x)≥0,即g(x)≤2
x-e恒成立.
故存在一次函数y=2
x-e,使得当x>0时,f(x)≥2
x-e,且g(x)≤2
x-e恒成立.
∴F′(x)=2(x-
| e |
| x |
| 2(x2-e) |
| x |
令F′(x)=0,得x=
| e |
| e |
∴当0<x<
| e |
| e |
当x>
| e |
| e |
∴当x=
| e |
即F(x)min=F(
| e |
| e |
∴F(x)的单调递增区间为(
| e |
| e |
(2)由(1)知,f(x)与g(x)的图象有且仅有一个公共点(
| e |
∴猜想:一次函数的图象就是f(x)与g(x)的图象在点(
| e |
其方程为y=2
| e |
下面证明:当x>0时,f(x)≥2
| e |
| e |
∵f(x)-(2
| e |
| e |
| e |
又令G(x)=2
| e |
| e |
| e |
| 2e |
| x |
2
| ||||
| x |
∴当0<x<
| e |
| e |
当x>
| e |
| e |
∴当x=
| e |
即G(x)min=G(
| e |
| e |
| e |
故存在一次函数y=2
| e |
| e |
| e |
点评:本题考查了,导数在求函数单调区间,求函数最值,证明恒成立问题.运用于数形结合思想,函数与方程思想,化归思想.是一道导数应用于的综合题,属于中档题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
已知命题:p:对任意x∈R,总有|x|≥0,q:x=1是方程x+2=0的根;则下列命题为真命题的是( )
| A、p∧¬q | B、¬p∧q |
| C、¬p∧¬q | D、p∧q |
设z=
+i,则|z|=( )
| 1 |
| 1+i |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
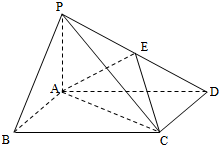 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.