题目内容
已知函数f（x）=
ax3-bx2+（2-b）x+1（a，b是实数，a≠0）在x=x1处取得极大值，在x=x2处取得极小值，且0＜x1＜1＜x2＜2．
（1）求证：0＜a＜2b＜3a：
（2）若函数g（x）=f′（x）-2+a-2b．设g（x）的零点为α，β，求|α-β|的取值范围．
| 1 |
| 3 |
（1）求证：0＜a＜2b＜3a：
（2）若函数g（x）=f′（x）-2+a-2b．设g（x）的零点为α，β，求|α-β|的取值范围．
考点：利用导数研究函数的极值
专题：计算题,证明题,导数的综合应用
分析：（1）由极值和导数的关系，以及单调性和导数的关系得到a＞0，再由二次函数的性质可得f′（0）＞0，f′（1）＜0，f′（2）＞0，即可得证；
（2）求出g（x）的表达式，运用韦达定理，求出|α-β|的表达式，配方再由（1）的结论，即可得到．
（2）求出g（x）的表达式，运用韦达定理，求出|α-β|的表达式，配方再由（1）的结论，即可得到．
解答：
（1）证明：由题意f'（x）=ax2-2bx+（2-b），
f'（x）=0的根为x1，x2，且0＜x1＜1＜x2＜2，
且f（x）在区间（-∞，x1），（x2，+∞）上单调递增，即f'（x）＞0，
f（x）在（x1，x2）上单调递减，即f'（x）＜0，
所以a＞0，
所以
?
＜
＜
，
又a＞0，所以0＜a＜2b＜3a；
（2）解：函数g（x）=f'（x）-2+a-2b．设g（x）的零点为α，β，
即有g（x）=ax2-2bx+a-3b，α+β=
，αβ=
，
则|α-β|=
=2
，
由（1）知
＜
＜
∴|α-β|∈(
)．
f'（x）=0的根为x1，x2，且0＜x1＜1＜x2＜2，
且f（x）在区间（-∞，x1），（x2，+∞）上单调递增，即f'（x）＞0，
f（x）在（x1，x2）上单调递减，即f'（x）＜0，
所以a＞0，
所以
|
| 1 |
| 2 |
| b |
| a |
| 3 |
| 2 |
又a＞0，所以0＜a＜2b＜3a；
（2）解：函数g（x）=f'（x）-2+a-2b．设g（x）的零点为α，β，
即有g（x）=ax2-2bx+a-3b，α+β=
| 2b |
| a |
| a-3b |
| a |
则|α-β|=
2
| ||
| |a| |
(
|
由（1）知
| 1 |
| 2 |
| b |
| a |
| 3 |
| 2 |
∴|α-β|∈(
| 3， |
| 23 |
点评：本题考查导数的综合应用：求单调区间和求极值，考查函数和方程的转换思想方法，注意运用二次函数的性质解决，属于中档题．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
相关题目
福建省第14届运动会在妈祖故里莆田举行，在开幕式表演“篮球操”的训练中我校A、B、C三个同学一组进行传球训练，每个同学传给另外两个中的某一个的可能性都相同
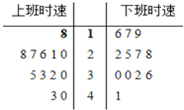某市对上下班交通情况作抽样调查，作出上下班时间各抽取的12辆机动车行驶时速（单位：km/h）的茎叶图如图．则上、下班行驶时速的中位数分别为（ ）| A、28与28.5 |
| B、29与28.5 |
| C、28与27.5 |
| D、29与27.5 |
如果a⊥b，那么a与b（ ）
| A、一定相交 | B、一定异面 |
| C、一定共面 | D、一定不平行 |