题目内容

8．设$p：{log_2}x＜0，q：{2^x}≥2$，则p是￢q的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分条件也不必要条件

分析 根据不等式的解法求出p，q的等价条件，结合充分条件和必要条件的定义进行判断．

解答 解：由log2x＜0得0＜x＜1，即p：0＜x＜1，
由2x≥2得x≥1，即q：x≥1，
则￢q：x＜1，
则p是￢q的充分不必要条件，
故选：A

点评 本题主要考查充分条件和必要条件的判断，求出p，q的等价条件是解决本题的关键．

练习册系列答案
相关题目
5．代数式sin75°cos75°的值为（　　）
A．$\frac{1}{4}$B．$-\frac{1}{4}$C．$\frac{{\sqrt{3}}}{4}$D．$-\frac{{\sqrt{3}}}{4}$
6．已知a∈R，若f（x）=（x+$\frac{a}{x}$-1）ex在区间（1，3）上有极值点，则a的取值范围是（-∞，-$\frac{27}{4}$）．
16．函数$f（x）=-|x|-\sqrt{x}+3$的零点所在区间为（　　）
A．（0，1）B．（1，2）C．（2，3）D．（3，4）
3．执行如图所示的程序框图，则输出的k值为（　　）
A．7B．9C．11D．13
13．一般来说，一个人脚越长，他的身高就越高．现对10名成年人的脚长x（单位：cm）与身高y（单位：cm）进行测量，得如下数据：
x20212223242526272829
y141146154160169176181188197203
作出散点图后，发现散点在一条直线附近．经计算得到一些数据：
$\overline{x}$=24.5，$\overline{y}$=171.5，$\sum_{i=1}^{10}$（xi-$\overline{x}$）（yi-$\overline{y}$）=577.5，$\sum_{i=1}^{10}$（xi-$\overline{x}$）2=82.5
某刑侦人员在某案发现场发现一对裸脚印，量得每个脚印长26.5cm，请你估计案发嫌疑人的身高为（　　）
A．185B．185.5C．186D．186.5
20．已知数列{an}的第1项为a1=1，且an+1=$\frac{{a}_{n}}{1+2{a}_{n}}$（n=1，2，3，4，…），通过计算a1，a2，a3，a4，猜想这个数列的通项公式为an=$\frac{1}{2n-1}$．
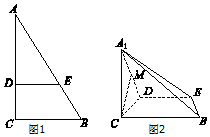17．如图1，在Rt△ABC中，∠C=90°，BC=6，AC=9，D，E分别为AC、AB上的点，且DE∥BC，DE=4，将△ADE沿DE折起到△A1DE的位置，使A1C⊥CD，如图2．
（1）求证：A1C⊥平面BCDE；
（2）若M是A1D的中点，求CM与平面A1BE所成角的正弦值．
18．若命题“p∨q”为真，且“￢p”为真，则（　　）
A．p或q为假B．q假C．q真D．不能判断q的真假

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网