题目内容
已知f(x)是定义在R上周期4π的偶函数,当x∈[0,π]时,f(x)=cosx,当x∈(π,2π]时,y=f(x)的图象是斜率为
且在y轴上的截距为-2的直线在相应区间上的部分.
(1)求出函数y=f(x)的表达式,
(2)写出函数y=f(x)的单调区间.
(3)求f(π)+f(2π)+f(3π)+…+f(2013π)的值.
| 2 |
| π |
(1)求出函数y=f(x)的表达式,
(2)写出函数y=f(x)的单调区间.
(3)求f(π)+f(2π)+f(3π)+…+f(2013π)的值.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:(1)根据函数f(x)是定义在R上周期4π的偶函数,求解解析式;(2)则结合余弦函数图象进行求解;(3)则利用函数的周期性进行求值.
解答:
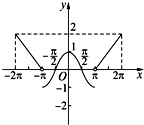
解:(1)设x∈[-2π,-π),
则-x∈(π,2π]f(x)是偶函数,
∵x∈(π,2π]时,y=f(x)=
x-2,
∴f(x)=f(-x)=-
x-2.
设x∈[-π,0]则-x∈[0,π],f(x)=f(-x)=cos(-x)=cosx
∴f(x)=
,
∴f(x)=
,
(2)
(3)
.

解:(1)设x∈[-2π,-π),
则-x∈(π,2π]f(x)是偶函数,
∵x∈(π,2π]时,y=f(x)=
| 2 |
| π |
∴f(x)=f(-x)=-
| 2 |
| π |
设x∈[-π,0]则-x∈[0,π],f(x)=f(-x)=cos(-x)=cosx
∴f(x)=
|
|
|
|
∴f(x)=
|
(2)
|
(3)
|
点评:本题综合考查三角函数的图象与性质、函数解析式求解等知识,考查比较综合.属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图已知函数y=Asin(ωx+φ)的部分图象,则表达式为( )
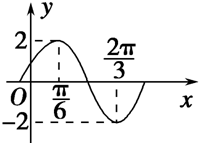

A、y=2sin(
| ||||
B、y=2sin(
| ||||
C、y=2sin(2x+
| ||||
D、y=2sin(2x-
|
 如图,射线OA,OB与x轴正半轴的夹角分别为45°和30°,过点P(1,0)的直线l分别交OA,OB于点A,B.
如图,射线OA,OB与x轴正半轴的夹角分别为45°和30°,过点P(1,0)的直线l分别交OA,OB于点A,B.