题目内容
方程lgx+x=0根的个数为（ ）
| A、无穷多 | B、3 | C、1 | D、0 |
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：由lgx+x=0，得lgx=-x，令f（x）=lgx，y=-x，画出两函数的图象，一目了然．
解答：
解；∵lgx+x=0，
∴lgx=-x，
令f（x）=lgx，y=-x，
画出函数的图象：
，
∴函数有一个交点，即方程有一个根，
故选：C．
∴lgx=-x，
令f（x）=lgx，y=-x，
画出函数的图象：
，∴函数有一个交点，即方程有一个根，
故选：C．
点评：本题考察了函数的根的存在性问题，渗透了转化思想，是一道基础题．
练习册系列答案
相关题目
设ξ的分布列为P（ξ=k）=C
（
）k（
）5-k，（k=0，1，2，3，4，5），求D（3ξ）=（ ）
k 5 |
| 1 |
| 3 |
| 2 |
| 3 |
| A、10 | B、30 | C、15 | D、5 |
若函数f（x）=ax3+bx2+cx+d的图象如图所示，则一定有（ ）
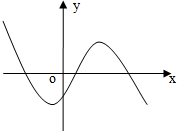
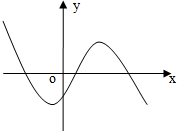
| A、a＜0 b＞0 c＞0 d＜0 |
| B、a＜0 b＜0 c＞0 d＜0 |
| C、a＜0 b＞0 c＜0 d＜0 |
| D、a＜0 b＜0 c＜0 d＜0 |
已知a＜b＜0，则下列不等式关系中不能成立的是（ ）
A、
| ||||
B、
| ||||
| C、|a|＞|b| | ||||
| D、a4＞b4 |
设正项等比数列{an}的前n项和为Sn，且210S30+S10=（210+1）S20，则数列{an}的公比为（ ）
| A、1 | ||
B、
| ||
C、
| ||
D、
|
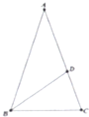学习“三角”时，小明同学在参考书上看到求sin18°精确值的一种方法，具体如下：设等腰△ABC的顶角∠A=36°．底角∠B的平分线交腰AC于D，且BC=1（如图），则AD=BD=1，于是，在△BCD中，可得CD=2sin18°．由△BAC∽△CBD得| AC |
| BC |
| BD |
| CD |
| 1+2sin18° |
| 1 |
| 1 |
| 2sin18° |
| ||
| 4 |
| π |
| 2 |
| 3π |
| 2 |
| π |
| 2 |
| A、关于x的方程α•4x+β•2x+α=0有实数解 | ||
| B、关于x的方程α•（log4x）2+β•log4x-α=0无实数解 | ||
C、关于x的方程sinx=
| ||
D、关于x的方程cosx=
|
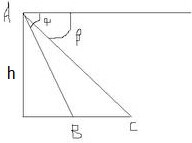如图，从高为h的气球（A）上测量铁桥（BC）的长，如果测得桥头B的俯角是α，桥头C的俯角是β，则该桥的长可表示为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|