题目内容
等比数列{an}中a1+a2+…+a5=15，a12+a22+…+a52=30，则a1-a2+a3-a4+a5=（ ）
| A、4 | B、3 | C、2 | D、1 |
考点：等比数列的前n项和
专题：等差数列与等比数列
分析：先设等比数列{an}公比为q，分别用a1和q表示出a12+a22+a32+a42+a52，a1+a2+a3+a4+a5和a1-a2+a3-a4+a5，发现a12+a22+a32+a42+a52除以a1+a2+a3+a4+a5正好与a1-a2+a3-a4+a5相等，进而得到答案．
解答：
解：设数列{an}的公比为q，且q≠1，则 a1+a2+a3+a4+a5=
=15 ①，
且 a12+a22+a32+a42+a52=
=30 ②．
∴②÷①得
=2，∴a1-a2+a3-a4+a5=
=2，
故选：C．
| a1(1-q5) |
| 1-q |
且 a12+a22+a32+a42+a52=
| a12(1-q10) |
| 1-q2 |
∴②÷①得
| a1(1+q5) |
| 1+q |
| a1(1+q5) |
| 1+q |
故选：C．
点评：本题主要考查了等比数列的性质，解题时要认真审题，注意等比数列的性质的灵活运用，属于基础题．．
练习册系列答案
活力课时同步练习册系列答案
相关题目
若a?α，b?α，a∥α，条件甲是“a∥b”，条件乙是“b∥α”，则条件甲是条件乙的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
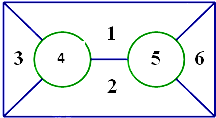有六种不同颜色，给如图的六个区域涂色，要求相邻区域不同色，不同的涂色方法共有（ ）| A、4320 | B、2880 |
| C、1440 | D、720 |
已知函数f（x）的导函数为f′（x），且满足f（x）=3f′（1）•x-x4，则f′（1）=（ ）
| A、-1 | B、-2 | C、1 | D、2 |
方程lgx+x=0根的个数为（ ）
| A、无穷多 | B、3 | C、1 | D、0 |
曲线f（x）=x2+3x在点A（1，4）处的切线斜率为（ ）
| A、2 | B、5 | C、6 | D、11 |
如果执行下面的算法语句后输出结果是8，则输入的值是（ ）
| A、3 | B、5或12- |
| C、12 | D、4或12 |
若函数f（x）=x3-3bx+3b在（0，2）内有极小值，则（ ）
| A、0＜b＜4 | ||
| B、b＜4 | ||
| C、b＞0 | ||
D、b＜
|