Question

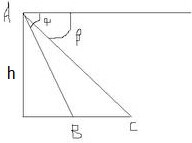如图，从高为h的气球（A）上测量铁桥（BC）的长，如果测得桥头B的俯角是α，桥头C的俯角是β，则该桥的长可表示为（　　）

• A、

  sin(α-β)

  sinαsinβ

  •h
• B、

  sin(α-β)

  cosαsinβ

  •h
• C、

  sin(α-β)

  cosαcosβ

  •h
• D、

  cos(α-β)

  cosαcosβ

  •h

Answer 1

考点：解三角形的实际应用

专题：计算题,解三角形

分析：先求出AB，再在△ABC中，求出BC．

解答： 解：由∠EAB=α，得∠DBA=α，
在Rt△ADB中，∵AD=h，
∴AB=

h

sinα

．
又∠EAC=β，∴∠BAC=α-β．
在△ABC中，BC=

ABsin(α-β)

sinβ

=

sin(α-β)

sinαsinβ

•h．
故选：A．

点评：本题考查了解三角形的实际应用，关键是把实际问题转化为数学问题，是中档题．