题目内容
边长分别为3,5,7的三角形的最大内角为( )
| A、150° | B、135° |
| C、120° | D、90° |
考点:余弦定理
专题:解三角形
分析:由题意可得三角形的最大内角即边7对的角,设为θ,由余弦定理可得 cosθ 的值,即可求得θ的值.
解答:
解:根据三角形中,大边对大角,故边长分别为3,5,7的三角形的最大内角即边7对的角,设为θ,
则由余弦定理可得 cosθ=
=-
,∴θ=120°,
故选:C.
则由余弦定理可得 cosθ=
| 32+52-72 |
| 2×3×5 |
| 1 |
| 2 |
故选:C.
点评:本题主要考查余弦定理的应用,大边对大角,二倍角公式,诱导公式,已知三角函数值求角的大小,属于基础题.

练习册系列答案
相关题目
已知一个算法,其流程图如图所示,则输出的结果是( )


| A、3 | B、9 | C、27 | D、81 |
若0<a<
,则下列不等式中正确的是( )
| 1 |
| 2 |
A、loga(1-
| ||
B、ax≤(
| ||
| C、cos(1+α)<cos(1-α) | ||
| D、(1-a)n<an(n∈N*) |
如果执行如图所示的程序框图,那么输出的s为( )


| A、2450 | B、2452 |
| C、2550 | D、2552 |
设x∈(0,π),则函数y=sinx+
的最小值是( )
| 1 |
| sinx |
| A、2 | ||
B、
| ||
C、
| ||
| D、3 |
一对年轻夫妇和其两岁的孩子做游戏,让孩子把分别写有“One”“World”,“One”,“Dream”的四张卡片随机排成一行,若卡片按从左到右的顺序排成“One World One Dream”,则孩子会得到父母的奖励,那么孩子受到奖励的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=
+lg(3x-1)的定义域是( )
| x2-1 | ||
|
| A、(-∞,-1) | ||
B、(-1,
| ||
C、(-
| ||
D、(
|
已知全集U=R,集合A={0,1,2,3,4,5},B=[2,+∞),则图中阴影部分所表示的集合( )
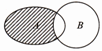

| A、{1} |
| B、{0,1} |
| C、{1,2} |
| D、{0,1,2} |