题目内容
15.下列结论判断正确的是( )| A. | 任意三点确定一个平面 | |
| B. | 任意四点确定一个平面 | |
| C. | 三条平行直线最多确定一个平面 | |
| D. | 正方体ABCD-A1B1C1D1中,AB与CC1异面 |
分析 根据题意,容易得出选项A、B、C错误,画出图形,结合异面直线的定义即可判断D正确.
解答  解:对于A,不在同一直线上的三点确定一个平面,∴命题A错误;
解:对于A,不在同一直线上的三点确定一个平面,∴命题A错误;
对于B,不在同一直线上的四点确定一个平面,∴命题B错误;
对于C,三条平行直线可以确定一个或三个平面,∴命题C错误;
对于D,如图所示,正方体ABCD-A1B1C1D1中,AB与CC1是异面直线,命题D正确.
故选:D.
点评 本题考查了平面的基本定理与异面直线的判定问题,解题时应熟练掌握平面基本定理与正方体的几何特征,是基础题.

练习册系列答案
相关题目
3.下列命题为真命题的是( )
| A. | 已知x,y∈R,则$\left\{\begin{array}{l}{x>1}\\{y>2}\end{array}\right.$是$\left\{\begin{array}{l}{x+y>3}\\{xy>2}\end{array}\right.$的充要条件 | |
| B. | 当0<x≤2时,函数y=x-$\frac{1}{x}$无最大值 | |
| C. | ?a,b∈R,$\frac{a+b}{2}≥\sqrt{ab}$ | |
| D. | ?x∈R,sinx+cosx=$\frac{7}{5}$ |
10.“x≤2或x≥5”是“x2-7x+10>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
20.设f(x)=1-cosx,则f′($\frac{π}{2}$)等于( )
| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
4.“m>0”是“x2+x+m=0无实根”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
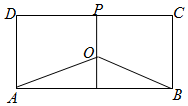 节能环保日益受到人们的重视,水污染治理也已成为“十三五”规划的重要议题.某地有三家工厂,分别位于矩形ABCD的两个顶点A、B及CD的中点P处,AB=30km,BC=15km,为了处理三家工厂的污水,现要在该矩形区域上(含边界),且与A、B等距离的一点O处,建造一个污水处理厂,并铺设三条排污管道AO、BO、PO.设∠BAO=x(弧度),排污管道的总长度为ykm.
节能环保日益受到人们的重视,水污染治理也已成为“十三五”规划的重要议题.某地有三家工厂,分别位于矩形ABCD的两个顶点A、B及CD的中点P处,AB=30km,BC=15km,为了处理三家工厂的污水,现要在该矩形区域上(含边界),且与A、B等距离的一点O处,建造一个污水处理厂,并铺设三条排污管道AO、BO、PO.设∠BAO=x(弧度),排污管道的总长度为ykm.