题目内容
5.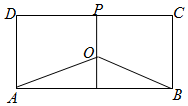 节能环保日益受到人们的重视,水污染治理也已成为“十三五”规划的重要议题.某地有三家工厂,分别位于矩形ABCD的两个顶点A、B及CD的中点P处,AB=30km,BC=15km,为了处理三家工厂的污水,现要在该矩形区域上(含边界),且与A、B等距离的一点O处,建造一个污水处理厂,并铺设三条排污管道AO、BO、PO.设∠BAO=x(弧度),排污管道的总长度为ykm.
节能环保日益受到人们的重视,水污染治理也已成为“十三五”规划的重要议题.某地有三家工厂,分别位于矩形ABCD的两个顶点A、B及CD的中点P处,AB=30km,BC=15km,为了处理三家工厂的污水,现要在该矩形区域上(含边界),且与A、B等距离的一点O处,建造一个污水处理厂,并铺设三条排污管道AO、BO、PO.设∠BAO=x(弧度),排污管道的总长度为ykm.(1)将y表示为x的函数;
(2)试确定O点的位置,使铺设的排污管道的总长度最短,并求总长度的最短公里数(精确到0.01km).
分析 (1)直接由已知条件求出AO、BO、OP的长度,即可得到所求函数关系式;
(2)记$p=\frac{2-sinx}{cosx}$,则sinx+pcosx=2,求出p的范围,即可得出结论.
解答 解:(1)由已知得$y=2×\frac{15}{cosx}+15-15tanx$,
即$y=15+15×\frac{2-sinx}{cosx}$(其中$0≤x≤\frac{π}{4}$)-----------------------------------------------(6分)
(2)记$p=\frac{2-sinx}{cosx}$,则sinx+pcosx=2,则有$|{\frac{2}{{\sqrt{1+{p^2}}}}}|≤1$,
解得$p≥\sqrt{3}$或$p≤-\sqrt{3}$------------------------------------------(10分)
由于y>0,所以,当$x=\frac{π}{6}$,即点O在CD中垂线上离点P距离为$({15-\frac{{15\sqrt{3}}}{3}})$km处,y取得最小值$15+15\sqrt{3}≈40.98$(km).-------------------------------------------------(14分)
点评 本题主要考查解三角形的实际应用,考查学生的计算能力.解决这类问题的关键在于把文字语言转换为数学符号,用数学知识解题.

练习册系列答案
相关题目
7.设函数y=f(cosx)是可导函数,则y′等于( )
| A. | f′(sinx) | B. | -f′(sinx) | C. | f′(cosx)sinx | D. | -f′(cosx)sinx |
17.已知定义域为R的偶函数f(x)的图象关于直线x=4对称,当x∈[0,4]时,f(x)可导且满足f′(x)>2f(x),则有( )
| A. | e2f(-15)<f(-6),e2f(-11)<f(-20) | B. | e2f(-15)>f(-6),e2f(-11)>f(-20) | ||
| C. | e2f(-15)<f(-6),e2f(-11)>f(-20) | D. | e2f(-15)>f(-6),e2f(-11)<f(-20) |
15.下列结论判断正确的是( )
| A. | 任意三点确定一个平面 | |
| B. | 任意四点确定一个平面 | |
| C. | 三条平行直线最多确定一个平面 | |
| D. | 正方体ABCD-A1B1C1D1中,AB与CC1异面 |