题目内容
5.已知直线l1的方程为3x-y+1=0,直线l2的方程为2x+y-3=0,则两直线l1与l2的夹角是$\frac{π}{4}$.分析 设直线l1与l2的夹角的大小为θ,求出直线的斜率,则由题意可得tanθ=|$\frac{3+2}{1+3×(-2)}$|=1,由此求得θ的值.
解答 解:设直线l1与l2的夹角的大小为θ,则θ∈[0,π),
由题意可得直线l1的斜率为3,直线l2的斜率为-2,
tanθ=|$\frac{3+2}{1+3×(-2)}$|=1,解得θ=$\frac{π}{4}$,
故答案为:$\frac{π}{4}$.
点评 本题主要考查两条直线的夹角公式的应用,属于中档题.

练习册系列答案
相关题目
15.下列结论判断正确的是( )
| A. | 任意三点确定一个平面 | |
| B. | 任意四点确定一个平面 | |
| C. | 三条平行直线最多确定一个平面 | |
| D. | 正方体ABCD-A1B1C1D1中,AB与CC1异面 |
20.过点(0,2b)的直线l与双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的一条斜率为正值的渐近线平行,若双曲线C的右支上的点到直线l的距离恒大于b,则双曲线C的离心率的取值范围是( )
| A. | (1,2] | B. | (2,+∞) | C. | (1,2) | D. | (1,$\sqrt{2}$] |
17.“$\frac{1}{x}$<3”是“x>$\frac{1}{3}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.已知实数a>1,命题p:函数$y=lo{g_{\frac{1}{2}}}({x^2}+2x+a)$的定义域为R,命题q:|x|<1是x<a的充分不必要条件,则( )
| A. | p或q为真命题 | B. | p且q为假命题 | C. | ¬p且q为真命题 | D. | ¬p或¬q为真命题 |
15.若非零向量$\overrightarrow a$,$\overrightarrow b$满足$|{\overrightarrow a}|=|{\overrightarrow b}|=|{\overrightarrow a+\overrightarrow b}|$,则$\overrightarrow a$与$\overrightarrow b$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
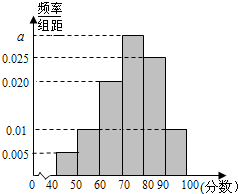 某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分