题目内容
6.给出以下结论:①有两个侧面是矩形的棱柱是直棱柱;
②有两个相邻侧面是矩形的棱柱是正棱柱;
③各侧面都是正方形的棱柱一定是正棱柱;
④一个三棱锥四个面可以都为直角三角形;
⑤长方体一条对角线与同一个顶点的三条棱所成的角为α,β,γ,则cos2α+cos2β+cos2γ=1.
其中正确的是④⑤(将正确结论的序号全填上)
分析 在①中,如果对面是矩形斜棱柱也可以做到;在②中,有两个相邻侧面是矩形的棱柱是直棱柱;在③中,底面一定是菱形,不一定是正方形;在④中,一个三棱锥四个面可以都为直角三角形;在⑤中,利用面对角线的性质求解.
解答 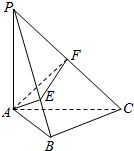 解:在①中,必须是相邻的两个侧面是矩形的棱柱才是直棱柱,
解:在①中,必须是相邻的两个侧面是矩形的棱柱才是直棱柱,
如果对面是矩形斜棱柱也可以做到,故①错误;
在②中,有两个相邻侧面是矩形的棱柱是直棱柱,不一定是正棱柱,故②错误;
在③中,各侧面都是正方形时,底面的四条边相等,
底面一定是菱形,不一定是正方形,
正棱柱的底面必须是正方形,故③错误;
在④中,一个三棱锥四个面可以都为直角三角形,
如右图,PA⊥平面ABC,AB⊥BC,
则三棱锥P-ABC的四个面都是直角三角形,故④正确;
在⑤中,设对角线B1D与长方体的棱AD、DC、D1D所成的角分别为α、β、γ,
连结AB1、CB1,D1B1,则△B1DA、△B1DC、△B1DD1都是直角三角形.
∵cosα=$\frac{DA}{D{B}_{1}}$,cosβ=$\frac{DC}{D{B}_{1}}$,cosγ=$\frac{D{D}_{1}}{D{B}_{1}}$,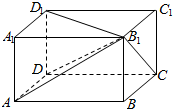
cos2α+cos2β+cos2γ=$\frac{D{A}^{2}+D{C}^{2}+D{{D}_{1}}^{2}}{D{B}^{2}}$=1.故⑤正确.
故答案为:④⑤.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
7.设函数y=f(cosx)是可导函数,则y′等于( )
| A. | f′(sinx) | B. | -f′(sinx) | C. | f′(cosx)sinx | D. | -f′(cosx)sinx |
17.已知定义域为R的偶函数f(x)的图象关于直线x=4对称,当x∈[0,4]时,f(x)可导且满足f′(x)>2f(x),则有( )
| A. | e2f(-15)<f(-6),e2f(-11)<f(-20) | B. | e2f(-15)>f(-6),e2f(-11)>f(-20) | ||
| C. | e2f(-15)<f(-6),e2f(-11)>f(-20) | D. | e2f(-15)>f(-6),e2f(-11)<f(-20) |
1.函数f(x)=x+lnx的零点个数是( )
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
15.下列结论判断正确的是( )
| A. | 任意三点确定一个平面 | |
| B. | 任意四点确定一个平面 | |
| C. | 三条平行直线最多确定一个平面 | |
| D. | 正方体ABCD-A1B1C1D1中,AB与CC1异面 |
 如图,ABCD是边长为a的正方形,PA⊥平面ABCD.
如图,ABCD是边长为a的正方形,PA⊥平面ABCD.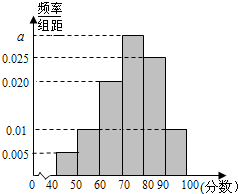 某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分