题目内容
8．已知集合A={x|$\frac{1-x}{1+x}$＞0}，B={x|lg（x+9）＜1}，则A∩B=（ ）| A． | （-1，1） | B． | （-∞，1） | C． | {0} | D． | {-1，0，1} |
分析 解不等式求得集合A，求函数定义域得集合B，根据交集的定义写出A∩B．
解答 解：集合A={x|$\frac{1-x}{1+x}$＞0}={x|（1-x）（1+x）＞0}={x|-1＜x＜1}，
B={x|lg（x+9）＜1}={x|0＜x+9＜10}={x|-9＜x＜1}，
则A∩B={x|-1＜x＜1}=（-1，1）．
故选：A．
点评 本题考查了集合的化简与运算问题，是基础题．
练习册系列答案
相关题目
18．若圆C：x2+y2=4上的点到直线l：y=x+a的最小距离为2，则a=（ ）
| A． | $2\sqrt{2}$ | B． | $4\sqrt{2}$ | C． | $±2\sqrt{2}$ | D． | $±4\sqrt{2}$ |
19．已知某几何体的三视图如图所示，则该几何体的体积为（ ）
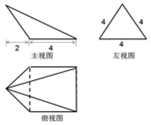
| A． | $\frac{32}{3}$ | B． | $\frac{{16\sqrt{3}}}{3}$ | C． | $\frac{{32\sqrt{3}}}{3}$ | D． | $\frac{{64\sqrt{3}}}{3}$ |
16．若tanα=$\frac{1}{3}$，则sin4α-cos4α+6sin$\frac{α}{2}$cos$\frac{α}{2}$cosα=（ ）
| A． | 1 | B． | $\frac{1}{3}$ | C． | $\frac{1}{9}$ | D． | $\frac{1}{10}$ |
13．已知方程$\frac{{x}^{2}}{2+m}$-$\frac{{y}^{2}}{m+1}$=1表示双曲线，则实数m的取值范围是（ ）
| A． | （-1，∞） | B． | （-2，-1） | C． | （-∞，-2）∪（-1，+∞） | D． | （-∞，-2） |
18．已知复数z1=1-i，z2=-2+3i，则复数$\frac{{i•{z_2}}}{z_1}$对应的点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |