题目内容
6.以坐标原点O为圆心,且与直线x+y+2=0相切的圆方程是x2+y2=2,圆O与圆x2+y2-2y-3=0的位置关系是相交.分析 由坐标原点为所求圆的圆心,且所求圆与已知直线垂直,利用点到直线的距离公式求出原点到已知直线的距离d,根据直线与圆相切时圆心到直线的距离等于圆的半径,即可得到所求圆的半径r,根据圆心和半径写出所求圆的方程即可;由两圆的圆心距为1,介于半径差与和之间,可得两圆相交.
解答 解:∵原点为所求圆的圆心,且所求圆与直线x+y+2=0相切,
∴所求圆的半径r=d=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$,
则所求圆的方程为x2+y2=2.
x2+y2-2y-3=0的圆心为(0,1),半径为2,两圆的圆心距为1,介于半径差与和之间,两圆相交.
故答案为:x2+y2=2;相交.
点评 此题考查了直线与圆的位置关系,圆的标准方程,以及点到直线的距离公式,直线与圆的位置相切时,圆心到直线的距离等于圆的半径,熟练掌握此性质是解本题的关键.

练习册系列答案
相关题目
17.已知圆O:x2+y2=4上三点A,B,C,且$\overrightarrow{OA}$=$\overrightarrow{BC}$,则$\overrightarrow{AC}$•$\overrightarrow{BA}$=( )
| A. | 6 | B. | -2$\sqrt{3}$ | C. | -6 | D. | 2$\sqrt{3}$ |
11.已知f(x)为奇函数,当x<0时,f(x)=a+x+log2(-x),其中a∈(-4,5),则f(4)>0的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
18.已知函数f(x)=$\frac{sin(\frac{2π}{3}-4x)}{cos(2x+\frac{π}{6})}$的图象与g(x)的图象关于直线x=$\frac{π}{12}$对称,则g(x)的图象的一个对称中心为( )
| A. | ($\frac{π}{6}$,0) | B. | ($\frac{π}{3}$,0) | C. | ($\frac{π}{4}$,0) | D. | ($\frac{π}{2}$,0) |
15.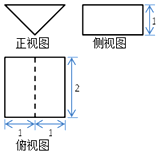 《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”.某“堑堵”的三视图如图,则它的表面积为( )
《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”.某“堑堵”的三视图如图,则它的表面积为( )
 《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”.某“堑堵”的三视图如图,则它的表面积为( )
《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”.某“堑堵”的三视图如图,则它的表面积为( )| A. | 2 | B. | 4+2$\sqrt{2}$ | C. | 4+4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
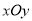 中,过点
中,过点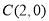 的直线与抛物线
的直线与抛物线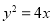 相交于点
相交于点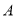 、
、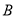 两点,设
两点,设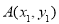 ,
,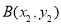 .
.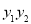 为定值;
为定值;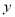 轴的定直线被以
轴的定直线被以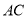 为直径的圆截得的弦长为定值?如果存在,求出该直线方程和弦长,如果不存在,说明理由.
为直径的圆截得的弦长为定值?如果存在,求出该直线方程和弦长,如果不存在,说明理由.