题目内容
15.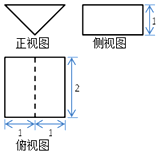 《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”.某“堑堵”的三视图如图,则它的表面积为( )
《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”.某“堑堵”的三视图如图,则它的表面积为( )| A. | 2 | B. | 4+2$\sqrt{2}$ | C. | 4+4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
分析 根据题意和三视图知几何体是一个放倒的直三棱柱,由三视图求出几何元素的长度,由面积公式求出几何体的表面积.
解答 解:根据题意和三视图知几何体是一个放倒的直三棱柱,底面是一个直角三角形,两条直角边分别是$\sqrt{2}$、斜边是2,且侧棱与底面垂直,侧棱长是2,
∴几何体的表面积S=$2×2+2×2×\sqrt{2}+2×\frac{1}{2}×\sqrt{2}×\sqrt{2}$=6+4$\sqrt{2}$,
故选:D.
点评 本题考查三视图求几何体的表面积,由三视图正确复原几何体是解题的关键,考查空间想象能力.

练习册系列答案
相关题目
7.已知椭圆x2+2y2=8的两个焦点分别为F1,F2,A为椭圆上的任意一点,AP是∠F1AF2的外角平分线,且$\overrightarrow{AP}•\overrightarrow{{F_2}P}=0$,则点P的坐标一定满足( )
| A. | x2+y2=8 | B. | x2+y2=1 | C. | x2-y2=1 | D. | $\frac{x^2}{4}+\frac{y^2}{3}=1$ |
20. 为了摸清整个江门大道的交通状况,工作人员随机选取20处路段,在给定的测试时间内记录到机动车的通行数量情况如下(单位:辆):
为了摸清整个江门大道的交通状况,工作人员随机选取20处路段,在给定的测试时间内记录到机动车的通行数量情况如下(单位:辆):
147 161 170 180 163 172 178 167 191 182
181 173 174 165 158 154 159 189 168 169
(Ⅰ)完成如下频数分布表,并作频率分布直方图;
(Ⅱ)现用分层抽样的方法从通行数量区间为[165,175)、[175,185)及[185,195)的路段中取出7处加以优化,再从这7处中随机选2处安装智能交通信号灯,设所取出的7处中,通行数量区间为[165,175)路段安装智能交通信号灯的数量为随机变量X(单位:盏),试求随机变量X的分布列与数学期望E(X).
 为了摸清整个江门大道的交通状况,工作人员随机选取20处路段,在给定的测试时间内记录到机动车的通行数量情况如下(单位:辆):
为了摸清整个江门大道的交通状况,工作人员随机选取20处路段,在给定的测试时间内记录到机动车的通行数量情况如下(单位:辆):147 161 170 180 163 172 178 167 191 182
181 173 174 165 158 154 159 189 168 169
(Ⅰ)完成如下频数分布表,并作频率分布直方图;
| 通行数量区间 | [145,155) | [155,165) | [165,175) | [175,185) | [185,195) |
| 频数 |
7.设函数f(x)=x2-2x-3,若从区间[-2,4]上任取一个实数x0,则所选取的实数x0满足f(x0)≤0的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
2.若点P是△ABC的外心,且$\overrightarrow{PA}$+$\overrightarrow{PB}$+λ$\overrightarrow{PC}$=$\overrightarrow{0}$,∠C=120°,则实数λ的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -1 | D. | 1 |
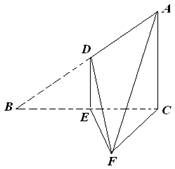 如图,直角△ABC中,∠ACB=90°,BC=2AC=4,D、E分别是AB、BC边的中点,沿DE将△BDE折起至△FDE,且∠CEF=60°.
如图,直角△ABC中,∠ACB=90°,BC=2AC=4,D、E分别是AB、BC边的中点,沿DE将△BDE折起至△FDE,且∠CEF=60°.