题目内容
20.已知函数f(x)=lnx-a(x-1),g(x)=ex(Ⅰ)若函数f(x)在区间(0,9]为增函数,求实数a的取值范围;
(Ⅱ)当a≠0时,过原点分别作曲线y=f(x)与y=g(x)的切线l1,l2,已知两切线的斜率互为倒数,证明:$\frac{e-1}{e}$<a<$\frac{{e}^{2}-1}{e}$.
分析 (Ⅰ)求出函数的导数,问题转化为即$\frac{1-ax}{x}$≥0在区间(0,9]恒成立,即a≤${[\frac{1}{x}]}_{min}$,求出a的范围即可;
(Ⅱ)设切线l2的方程为y=k2x,从而由导数及斜率公式可求得切点为(1,e),k2=e;再设l1的方程为y=$\frac{1}{e}$x;设l1与曲线y=f(x)的切点为(x1,y1),从而可得y1=$\frac{{x}_{1}}{e}$=1-ax1,a=$\frac{1}{{x}_{1}}$-$\frac{1}{e}$;结合y1=lnx1-a(x1-1)可得lnx1-1+$\frac{1}{{x}_{1}}$-$\frac{1}{e}$=0,再令m(x)=lnx-1+$\frac{1}{x}$-$\frac{1}{e}$,从而求导确定函数的单调性,从而确定$\frac{e-1}{e}$<a<$\frac{{e}^{2}-1}{e}$,问题得证.
解答 解:(Ⅰ)由f(x)=lnx-a(x-1)得,
f′(x)=$\frac{1}{x}$-a=$\frac{1-ax}{x}$,
∵函数f(x)在区间(0,9]为增函数,
∴f′(x)≥0在区间(0,9]恒成立,
即$\frac{1-ax}{x}$≥0在区间(0,9]恒成立,
∴a≤${[\frac{1}{x}]}_{min}$,而${[\frac{1}{x}]}_{min}$=$\frac{1}{9}$,
∴a∈(-∞,$\frac{1}{9}$];
(Ⅱ)证明:设切线l2的方程为y=k2x,切点为(x2,y2),则y2=ex2,
k2=g′(x2)=ex2=$\frac{{y}_{2}}{{x}_{2}}$,
所以x2=1,y2=e,则k2=e.
由题意知,切线l1的斜率为k1=$\frac{1}{{k}_{2}}$=$\frac{1}{e}$,l1的方程为y=$\frac{1}{e}$x;
设l1与曲线y=f(x)的切点为(x1,y1),则k1=f′(x1)=$\frac{1}{{x}_{1}}$-a=$\frac{1}{e}$=$\frac{{y}_{1}}{{x}_{1}}$,
所以y1=$\frac{{x}_{1}}{e}$=1-ax1,a=$\frac{1}{{x}_{1}}$-$\frac{1}{e}$.
又因为y1=lnx1-a(x1-1),消去y1和a后,
整理得lnx1-1+$\frac{1}{{x}_{1}}$-$\frac{1}{e}$=0.
令m(x)=lnx-1+$\frac{1}{x}$-$\frac{1}{e}$=0,
则m′(x)=$\frac{1}{x}$-$\frac{1}{{x}^{2}}$=$\frac{x-1}{{x}^{2}}$,m(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
若x1∈(0,1),因为m($\frac{1}{e}$)=-2+e-$\frac{1}{e}$>0,m(1)=-$\frac{1}{e}$<0,所以x1∈($\frac{1}{e}$,1),
而a=$\frac{1}{{x}_{1}}$-$\frac{1}{e}$在x1∈($\frac{1}{e}$,1)上单调递减,所以 $\frac{e-1}{e}$<a<$\frac{{e}^{2}-1}{e}$.
若x1∈(1,+∞),因为m(x)在(1,+∞)上单调递增,且m(e)=0,则x1=e,
所以a=$\frac{1}{{x}_{1}}$-$\frac{1}{e}$=0(舍去).
综上可知,$\frac{e-1}{e}$<a<$\frac{{e}^{2}-1}{e}$.
点评 本题考查利用导数讨论含参数函数的单调性、利用导数求曲线的切线问题,主要考查利用导函数研究曲线的切线及结合方程有解零点存在定理的应该用求参数的问题,得到不等式的证明;属于难题.

| A. | x2+y2=8 | B. | x2+y2=1 | C. | x2-y2=1 | D. | $\frac{x^2}{4}+\frac{y^2}{3}=1$ |
 满足约束条件
满足约束条件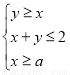 ,且
,且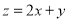 的最大值是最小值的3倍,则
的最大值是最小值的3倍,则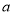 的值是( )
的值是( ) B.
B.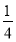
 为等差数列,
为等差数列, 为前
为前 项和,公差为
项和,公差为 ,若
,若 ,则
,则 的值为( )
的值为( ) B.
B.
 D.
D.
 如图所示,MA⊥平面ABCD,底面ABCD边长为1的正方形,MA=2AB,P是MC上一点,且$\overrightarrow{CP}$=$\frac{1}{5}$$\overrightarrow{CM}$
如图所示,MA⊥平面ABCD,底面ABCD边长为1的正方形,MA=2AB,P是MC上一点,且$\overrightarrow{CP}$=$\frac{1}{5}$$\overrightarrow{CM}$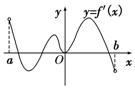 已知函数f(x)的定义域为(a,b),导函数f′(x)在(a,b)上的图象如图所示,则函数f(x)在(a,b)上的极大值点的个数为( )
已知函数f(x)的定义域为(a,b),导函数f′(x)在(a,b)上的图象如图所示,则函数f(x)在(a,b)上的极大值点的个数为( )