题目内容
20.曲线$y=lnx-\frac{2}{x}$在x=1处的切线的倾斜角为α,则cosα+sinα的值为( )| A. | $\frac{{2\sqrt{10}}}{5}$ | B. | $\frac{{\sqrt{10}}}{10}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\frac{{3\sqrt{10}}}{10}$ |
分析 通过函数的导数求出切线的斜率,求出切线的倾斜角的正切值,结合同角基本关系式,解方程,即可得到所求和.
解答 解:f(x)=lnx-$\frac{2}{x}$,
∴函数f′(x)=$\frac{1}{x}$+$\frac{2}{{x}^{2}}$,
∵y=f(x)在x=1处的切线的倾斜角为α,
∴tanα=3,0<α<$\frac{π}{2}$,即sinα=3cosα,
又sin2α+cos2α=1,
解得sinα=$\frac{3}{\sqrt{10}}$,cosα=$\frac{1}{\sqrt{10}}$,
∴cosα+sinα的值为$\frac{4}{\sqrt{10}}$=$\frac{2\sqrt{10}}{5}$.
故选:A.
点评 本题考查导数的几何意义,考查切线方程,考查同角的三角函数的基本关系式,学生的计算能力,属于基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
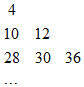 设数列{an}是集合{x|x=3s+3t,s<t且s,t∈N}中所有的数从小到大排列成的数列,即a1=4,a2=10,a3=12,a4=28,a5=30,a6=36,…,将数列{an}中各项按照上小下大,左小右大的原则排成如图的等腰直角三角形数表,则a15的值为324.
设数列{an}是集合{x|x=3s+3t,s<t且s,t∈N}中所有的数从小到大排列成的数列,即a1=4,a2=10,a3=12,a4=28,a5=30,a6=36,…,将数列{an}中各项按照上小下大,左小右大的原则排成如图的等腰直角三角形数表,则a15的值为324.