题目内容
已知集合A={x|x2+x-2<0},集合B={x|(x+2)(3-x)>0},则(∁RA)∩B等于( )
| A、{x|1≤x<3} |
| B、{x|2≤x<3} |
| C、{x|-2<x<1} |
| D、{x|-2<x≤-1或2≤x<3} |
考点:交、并、补集的混合运算
专题:集合
分析:求出A与B中不等式的解集确定出B,求出A的补集,找出补集与B的公共部分,能求出结果.
解答:
解:∵集合A={x|x2+x-2<0}={x|-2<x<1},
集合B={x|(x+2)(3-x)>0}={x|-2<x<3},
∴(CRA)∩B={x|x≤-2或x≥1}∩{x|-2<x<3}
={x|1≤x<3}.
故选:A.

集合B={x|(x+2)(3-x)>0}={x|-2<x<3},
∴(CRA)∩B={x|x≤-2或x≥1}∩{x|-2<x<3}
={x|1≤x<3}.
故选:A.
点评:此题考查了补集及其运算,熟练掌握补集的定义是解本题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
在△ABC中,角A,B,C所对的边分别为a,b,c,已知角A=30°,a=8,b=8
,则△ABC的面积等于
( )
| 3 |
( )
A、32
| ||||
B、32
| ||||
C、32
| ||||
D、64
|
已知直线ax+by+1=0中的a,b是取自集合{-3,-2,-1,0,1,2}中的2个不同的元素,并且直线的倾斜角大于60°,那么符合这些条件的直线共有( )
| A、16条 | B、13条 |
| C、11条 | D、8条 |
已知y=f(x)是定义域为R的奇函数,且当x>0时,f(x)=2x+x3-4.若存在x0∈I,使得f(x0)=0,则区间I不可能是( )
| A、(-2,-1) |
| B、(-1,1) |
| C、(1,2) |
| D、(-1,0) |
已知函数f(x)=
sin(2x+ϕ),若f(a)=
,则f(a+
)与f(a+
)的大小关系是( )
| 3 |
| 3 |
| 5π |
| 6 |
| π |
| 12 |
A、f(a+
| ||||
B、f(a+
| ||||
C、f(a+
| ||||
| D、大小与a、ϕ有关 |
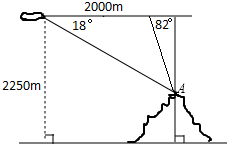 如图,一只气球在2250m的高空水平飞行,气球上的工作人员测得前方一座山顶上A点处的俯角为18°,当气球向前飞行了2000m后,又测得前方A点处的俯角为82°,则山的高度为
如图,一只气球在2250m的高空水平飞行,气球上的工作人员测得前方一座山顶上A点处的俯角为18°,当气球向前飞行了2000m后,又测得前方A点处的俯角为82°,则山的高度为