题目内容
已知函数f(x)=x3+ax2+bx在x=1处有极值-2.
(1)求常数a、b;
(2)求曲线y=
与直线y=x-1所围成图形的面积.
(1)求常数a、b;
(2)求曲线y=
| f(x) |
| x |
考点:利用导数研究函数的极值,定积分
专题:导数的综合应用
分析:(1)求f′(x),根据极值的定义即可建立关于a,b的方程组,解方程组即得a,b;
(2)先求出曲线方程:y=x2-3,联立直线方程y=x-1求出x=-1,或2,所以根据定积分的几何意义即得面积为:∫-12[x-1-(x2-3)],求出这个定积分即可.
(2)先求出曲线方程:y=x2-3,联立直线方程y=x-1求出x=-1,或2,所以根据定积分的几何意义即得面积为:∫-12[x-1-(x2-3)],求出这个定积分即可.
解答:
解:(1)f′(x)=3x2+2ax+b,∵函数f(x)在x=1处有极值-2,∴得到:
,解得a=0,b=-3;
(2)y=
=x2-3,∴解
得x=-1,或2,画出y=x2-3与y=x-1的图象如下图:
 ∴曲线y=
∴曲线y=
与直线y=x-1所围成图形的面积为:
∫-12(x-1-x2+3)dx=(-
x3+
x2+2x)|-12=
.
|
(2)y=
| f(x) |
| x |
|
 ∴曲线y=
∴曲线y=| f(x) |
| x |
∫-12(x-1-x2+3)dx=(-
| 1 |
| 3 |
| 1 |
| 2 |
| 9 |
| 2 |
点评:考查极值的概念,用定积分求曲线和直线所围成面积.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
如果复数z1=a+6i,z2=3-4i,且
为纯虚数,那么实数a的值为( )
| z1 |
| z2 |
A、-
| ||
| B、0 | ||
| C、2 | ||
| D、8 |
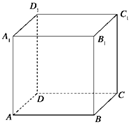 如图已知正方体ABCD-A1B1C1D1的棱长为3,点M在AC上,点N在BC1上,且|AM|=2|MC|,|BN|=2|NC|.
如图已知正方体ABCD-A1B1C1D1的棱长为3,点M在AC上,点N在BC1上,且|AM|=2|MC|,|BN|=2|NC|.