题目内容
求以椭圆
+
=1的两个顶点为焦点,以椭圆的焦点为顶点的双曲线方程,并求此双曲线的实轴长、虚轴长、离心率及渐近线方程.
| x2 |
| 16 |
| y2 |
| 9 |
考点:双曲线的简单性质,椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:确定椭圆的焦点、顶点坐标,可得双曲线的顶点、焦点坐标,即可求出双曲线的离心率、渐近线方程.
解答:
解:椭圆的焦点F1(-
,0),F2(
,0),即为双曲线的顶点.
∵双曲线的顶点和焦点在同一直线上,
∴双曲线的焦点应为椭圆长轴的端点A1(-4,0),A2(4,0),∴c=4,a=
,
∴b=3,
故所求双曲线的方程为
-
=1.…(6分)
实轴长为2a=2
,虚轴长为2b=6,
离心率e=
=
,渐近线方程为y=±
x.…(12分)
| 7 |
| 7 |
∵双曲线的顶点和焦点在同一直线上,
∴双曲线的焦点应为椭圆长轴的端点A1(-4,0),A2(4,0),∴c=4,a=
| 7 |
∴b=3,
故所求双曲线的方程为
| x2 |
| 7 |
| y2 |
| 9 |
实轴长为2a=2
| 7 |
离心率e=
| c |
| a |
4
| ||
| 7 |
3
| ||
| 7 |
点评:本题考查双曲线的方程与性质,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
复数(1-2i)2的虚部为( )
| A、-4 | B、-2 | C、2 | D、2i |
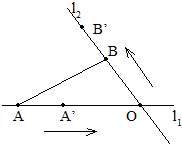 为进行科学实验,观测小球A、B在两条相交成60°角的直线型轨道上运动的情况,如图所示,运动开始前,A和B分别距O点3m和1m,后来它们同时以每分钟4m的速度各沿轨道l1、l2按箭头的方向运动.问:
为进行科学实验,观测小球A、B在两条相交成60°角的直线型轨道上运动的情况,如图所示,运动开始前,A和B分别距O点3m和1m,后来它们同时以每分钟4m的速度各沿轨道l1、l2按箭头的方向运动.问: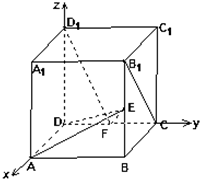 在正方体ABCD-A1B1C1D1中,如图E、F分别是BB1,CD的中点,
在正方体ABCD-A1B1C1D1中,如图E、F分别是BB1,CD的中点,