题目内容
证明下列不等式:
(1)若a>0,b>0,且
+
=1,求证:a+b≥4.
(2)若b>a>0,求证:ln
<
-1.
(1)若a>0,b>0,且
| 1 |
| a |
| 1 |
| b |
(2)若b>a>0,求证:ln
| b |
| a |
| b |
| a |
考点:不等式的证明,基本不等式
专题:不等式的解法及应用
分析:(1)利用基本不等式,可得a+b=(a+b)•(
+
)=2+
+
≥2+2
=4,从而可证得结论成立;
(2)设g(x)=lnx-(x-1)(x>1),利用g′(x)=
-1知,x>1时,g′(x)<0,g(x)=lnx-(x-1)(x>1)在[1,+∞)上递减,令x=
(b>a>0),即可证得结论成立.
| 1 |
| a |
| 1 |
| b |
| b |
| a |
| a |
| b |
|
(2)设g(x)=lnx-(x-1)(x>1),利用g′(x)=
| 1 |
| x |
| b |
| a |
解答:
证明:(1)∵a>0,b>0,且
+
=1,
∴a+b=(a+b)•(
+
)=2+
+
≥2+2
=4,当且仅当即a=b时取等号.(6分)
(2)设g(x)=lnx-(x-1)(x>1)…(8分)
∴g′(x)=
-1,
∴x>1时,g′(x)<0,g(x)=lnx-(x-1)(x>1)在[1,+∞)上递减,
又g(1)=ln1-(1-1)=0,
∴x>1时g(x)<g(1)=0即lnx<(x-1),
令x=
(b>a>0),
则ln
<
-1. …(13分
| 1 |
| a |
| 1 |
| b |
∴a+b=(a+b)•(
| 1 |
| a |
| 1 |
| b |
| b |
| a |
| a |
| b |
|
(2)设g(x)=lnx-(x-1)(x>1)…(8分)
∴g′(x)=
| 1 |
| x |
∴x>1时,g′(x)<0,g(x)=lnx-(x-1)(x>1)在[1,+∞)上递减,
又g(1)=ln1-(1-1)=0,
∴x>1时g(x)<g(1)=0即lnx<(x-1),
令x=
| b |
| a |
则ln
| b |
| a |
| b |
| a |
点评:本题考查不等式的证明,着重考查基本不等式的应用及推理证明能力,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
已知函数y=3sin(2x+
),则它的一条对称轴方程为( )
| π |
| 6 |
| A、x=0 | ||
B、x=-
| ||
C、x=
| ||
D、x=
|
 已知四棱锥P-ABCD,四边形ABCD为矩形,且PA⊥ABCD,E,F是PB的三等分点,E,F在PB上,PA=12,DC=9,BD=5,求异面直线DE与CF的夹角.
已知四棱锥P-ABCD,四边形ABCD为矩形,且PA⊥ABCD,E,F是PB的三等分点,E,F在PB上,PA=12,DC=9,BD=5,求异面直线DE与CF的夹角.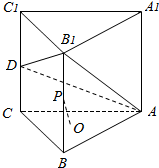 三棱柱ABC-A1B1C1中,点D、P为棱CC1、BB1的中点,O为△ABC重心,求证:OP∥平面AB1D.
三棱柱ABC-A1B1C1中,点D、P为棱CC1、BB1的中点,O为△ABC重心,求证:OP∥平面AB1D.