题目内容
已知四棱锥P-ABCD，四边形ABCD为矩形，且PA⊥ABCD，E，F是PB的三等分点，E，F在PB上，PA=12，DC=9，BD=5，求异面直线DE与CF的夹角．考点：异面直线及其所成的角
专题：空间角
分析：以A为原点，AC为x轴，AB为y轴．AP为z轴，建立空间直角坐标系，利用向量法能求出异面直线DE与CF的夹角．
解答：
解：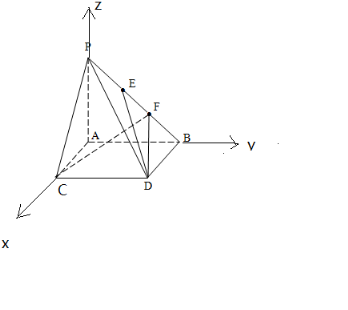
以A为原点，AC为x轴，AB为y轴．AP为z轴，
建立空间直角坐标系，
则由题意知D（5，9，0），C（5，0，0），
P（0，0，12），B（0，9，0），
∴
=(0，9，-12)，
=
=(0，3，-4)，
=
=（0，6，-8），
∴E（0，3，8），F（0，6，4），
∴
=(-5，-6，8)，
=(-5，6，4)，
设异面直线DE与CF的夹角为θ，
则cosθ=|cos＜
，
＞|
=|
|=
．
∴异面直线DE与CF的夹角为arccos
．
以A为原点，AC为x轴，AB为y轴．AP为z轴，建立空间直角坐标系，
则由题意知D（5，9，0），C（5，0，0），
P（0，0，12），B（0，9，0），
∴
| PB |
| PE |
| 1 |
| 3 |
| PB |
| PF |
| 2 |
| 3 |
| PB |
∴E（0，3，8），F（0，6，4），
∴
| DE |
| CF |
设异面直线DE与CF的夹角为θ，
则cosθ=|cos＜
| DE |
| CF |
=|
| 25-36+32 | ||||
|
21
| ||
| 1925 |
∴异面直线DE与CF的夹角为arccos
21
| ||
| 1925 |
点评：本题考查异面直线的夹角的求法，是中档题，解题时要认真审题，注意向量法的合理运用．
练习册系列答案
春雨教育同步作文系列答案
相关题目
若平面向量
=（1，-2）与
的夹角为π，且|
|=3
，则
的坐标为（ ）
| a |
| b |
| b |
| 5 |
| b |
| A、（3，-6） |
| B、（-3，6） |
| C、（6，-3） |
| D、（-6，3） |
如图：已知三棱锥P-ABC中，PA⊥面ABC，AB⊥AC，PA=AC=
已知椭圆C：
如图，在长方体ABCD-A1B1C1D1中，AB=AD=1，AA1=2．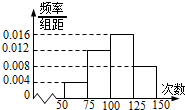
为了了解初中生的身体素质，某地区随机抽取了n名学生进行跳绳测试，根据所得数据画样本的频率分布直方图如图所示，且从左到右第一小组的频数是10，则n的值为