题目内容
(本小题满分14分)如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A、B的一点.
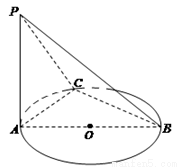
(1)求证:平面PAC⊥平面PBC;
(2)若PA=AB=2,∠ABC=30°,求三棱锥P-ABC的体积.
(1)(2)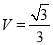
【解析】
试题分析:(1)由已知可得PA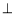 BC,AC
BC,AC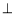 BC,再由直线与平面垂直的判定定理证得BC
BC,再由直线与平面垂直的判定定理证得BC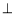 平面PAC,
平面PAC,
最后由平面与平面垂直的判定定理可得平面PAC⊥平面PBC
(2)∵PA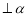 ,∴三棱锥P-ABC的体积
,∴三棱锥P-ABC的体积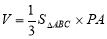 ,由已知PA=AB=2,∠ABC=30°可求
,由已知PA=AB=2,∠ABC=30°可求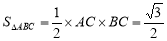 ,则体积可求.
,则体积可求.
试题解析:(1)设⊙O所在的平面为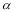 ,
,
依题意,PA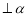 ,BC
,BC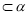 ,∴PA
,∴PA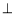 BC
BC
∵AB是⊙O的直径,C是圆周上不同于A、B的一点,∴AC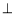 BC
BC
∵PA∩AC=A,∴BC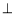 平面PAC
平面PAC
∵BC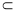 平面PBC,∴平面PAC⊥平面PBC
平面PBC,∴平面PAC⊥平面PBC
(2)∵PA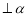 ,∴三棱锥P-ABC的体积
,∴三棱锥P-ABC的体积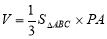
∵AB=2,∠ABC=30°,AC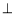 BC,∴AC=1,BC=
BC,∴AC=1,BC=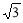
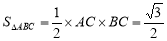
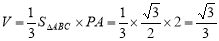
考点:直线与平面垂直的判定定理,平面与平面垂直的判定定理,椎体体积公式

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 ,现要在其中圈出一块矩形场地ABCD作为儿童乐园使用,其中点A、B在弧MN上,且线段AB平行于线段MN
,现要在其中圈出一块矩形场地ABCD作为儿童乐园使用,其中点A、B在弧MN上,且线段AB平行于线段MN
 中,
中,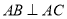 ,
, ,
,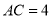 ,动点
,动点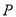 满足
满足 ,当
,当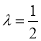 时,
时,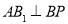 .
.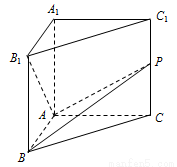
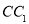 的长;
的长;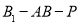 的大小为
的大小为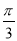 ,求
,求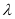 的值..
的值..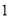 ,侧面积是底面积的
,侧面积是底面积的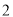 倍,则该圆锥的体积为 .
倍,则该圆锥的体积为 . ,集合
,集合 ,若
,若 ,则
,则 .
. ,
, 满足约束条件
满足约束条件 ,则
,则 的最小值为 .
的最小值为 .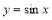 上所有的点横坐标伸长到原来的2倍,纵坐标不变,所得曲线对应的函数的最小正周期
上所有的点横坐标伸长到原来的2倍,纵坐标不变,所得曲线对应的函数的最小正周期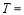
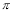 B.
B.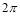 C.
C.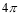 D.
D.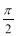
 的离心率
的离心率 .
. ,则
,则 .
.