题目内容
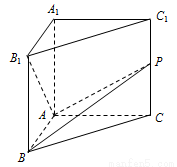
(本题满分10分)如图,在直三棱柱 中,
中,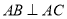 ,
, ,
,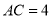 ,动点
,动点 满足
满足 ,当
,当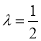 时,
时,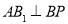 .
.
(1)求棱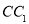 的长;
的长;
(2)若二面角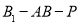 的大小为
的大小为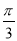 ,求
,求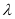 的值..
的值..
(Ⅰ) (Ⅱ)
(Ⅱ)
【解析】
试题分析:(Ⅰ)利用空间向量化简线线垂直条件,就是计算其数量积为零:设 ,
, 当
当 时,有
时,有 解得
解得 ,即棱
,即棱 的长为
的长为 .(Ⅱ)先求平面平面
.(Ⅱ)先求平面平面 的一个法向量为
的一个法向量为 ,而平面
,而平面 的一个法向量为
的一个法向量为 ,再根据两法向量夹角与二面角关系列等量关系:
,再根据两法向量夹角与二面角关系列等量关系:
 ,结合
,结合 ,解得
,解得 . 、
. 、
试题解析:(1)以点 为坐标原点,
为坐标原点, 分别为
分别为 轴,
轴,
建立空间直角坐标系,
设 ,则
,则 ,
, ,
, ,
,
所以 ,
, ,
, , 2分
, 2分
当 时,有
时,有
解得 ,即棱
,即棱 的长为
的长为 . 4分
. 4分
(2)设平面 的一个法向量为
的一个法向量为 ,
,
则由 ,得
,得 ,即
,即 ,
,
令 ,则
,则 ,所以平面
,所以平面 的一个法向量为
的一个法向量为 , 6分
, 6分
又平面 与
与 轴垂直,所以平面
轴垂直,所以平面 的一个法向量为
的一个法向量为 ,
,
因二面角 的平面角的大小为
的平面角的大小为 ,
,
所以 ,结合
,结合 ,解得
,解得 . 10分
. 10分
考点:利用空间向量证明研究二面角

练习册系列答案
相关题目
 在
在 是减函数,则
是减函数,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 ,若
,若 与
与 平行,则实数
平行,则实数 =_________.
=_________. ,
, ,则“
,则“ ”是“
”是“ ”成立的 条件 (选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”) .
”成立的 条件 (选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”) .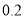 ,甲、乙下和棋的概率为
,甲、乙下和棋的概率为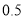 ,则乙获胜的概率为 .
,则乙获胜的概率为 . ,
, .
.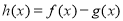 .
. 在
在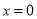 处的切线过点
处的切线过点 ,求
,求 的值;
的值; 时,若函数
时,若函数 上没有零点,求
上没有零点,求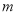 的取值范围;
的取值范围; ,且
,且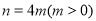 ,求证:当
,求证:当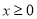 时,
时,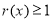 .
. 是定义在
是定义在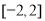 上的奇函数,当
上的奇函数,当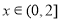 时,
时, ,函数
,函数 . 如果对于
. 如果对于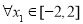 ,
,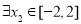 ,使得
,使得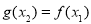 ,则实数
,则实数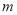 的取值范围是 .
的取值范围是 .
 中,底面
中,底面 为正方形,
为正方形, //
// //
// ,
, ,且
,且 .
.
 //
// ;
; .
.