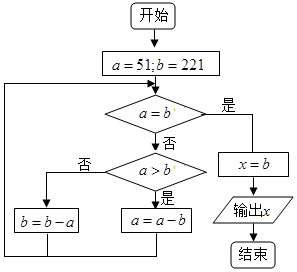
题目内容
16.若实数a,b,c满足(a-2b-1)2+(a-c-lnc)2=0,则|b-c|的最小值是1.分析 (a-2b-1)2+(a-c-lnc)2=0,可得a=2b+1,a=c+lnc.2b+1=c+lnc,|b-c|=$\frac{|1+c-lnc|}{2}$,令f(c)=1+c-lnc(c>0),利用导数研究函数的单调性极值与最值即可得出.
解答 解:∵(a-2b-1)2+(a-c-lnc)2=0,∴a=2b+1,a=c+lnc.
∴2b+1=c+lnc,
b=$\frac{c+lnc-1}{2}$.
∴|b-c|=$\frac{|1+c-lnc|}{2}$,
令f(c)=1+c-lnc(c>0),
f′(c)=1-$\frac{1}{c}$=$\frac{c-1}{c}$,
可得:c=1时,函数f(c)取得极小值即最小值,f(1)=2>0.
∴|b-c|=$\frac{|1+c-lnc|}{2}$≥1,
故答案为:1.
点评 本题考查了利用导数研究函数的单调性极值与最值、函数的性质、方程的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
7.在(x-$\frac{1}{x}$)10的二项展开式中,x4的系数等于( )
| A. | -120 | B. | -60 | C. | 60 | D. | 120 |
4.已知集合A={x|x2-5x-6≤0},$B=\left\{{\left.x\right|\frac{1}{x-1}>0}\right\}$,则A∩B等于( )
| A. | [-1,6] | B. | (1,6] | C. | [-1,+∞) | D. | [2,3] |
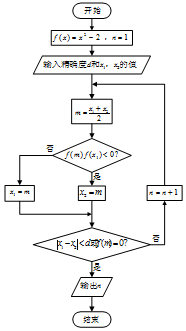 二分法是求方程近似解的一种方法,其原理是“一分为二,无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.1,则输出n的值为( )
二分法是求方程近似解的一种方法,其原理是“一分为二,无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.1,则输出n的值为( )