题目内容
6.已知函数f(x)=kx,g(x)=2lnx+2e($\frac{1}{e}$≤x≤e2),若f(x)与g(x)的图象上分别存在点M,N,使得MN关于直线y=e对称,则实数k的取值范围是[-$\frac{2}{e}$,2e].分析 设M(x,kx),则N(x,2e-kx),推导出k=-$\frac{2}{x}$lnx,由此利用导数性质能求出实数k的取值范围.
解答 解:∵函数f(x)=kx,g(x)=2lnx+2e($\frac{1}{e}$≤x≤e2),
f(x)与g(x)的图象上分别存在点M,N,使得M,N关于直线y=e对称,
∴设M(x,kx),则N(x,2e-kx),
∴2e-kx=2lnx+2e,∴k=-$\frac{2}{x}$lnx,
k′=$\frac{-2+2lnx}{{x}^{2}}$,由k′=0,得x=e,
∵$\frac{1}{e}$≤x≤e2,∴x∈[$\frac{1}{e}$,e)时,k′<0,k=-$\frac{2}{x}$lnx是减函数;
x∈(e,e2]时,k′>0,k=-$\frac{2}{x}$lnx是增函数,
∴x=e时,k=-$\frac{2}{e}$lne=-$\frac{2}{e}$;x=e2时,k=-$\frac{2}{{e}^{2}}$lne2=-$\frac{4}{{e}^{2}}$;x=$\frac{1}{e}$时,k=-$\frac{2}{\frac{1}{e}}$ln$\frac{1}{e}$=2e,
∴kmin=-$\frac{2}{e}$,kmax=2e.
∴实数k的取值范围是[-$\frac{2}{e}$,2e].
故答案为:$[-\frac{2}{e},2e]$
点评 本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
17.如图为某几何体的三视图,则其体积为( )
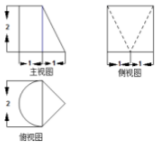

| A. | π+$\frac{4}{3}$ | B. | $\frac{π}{3}$+4 | C. | $\frac{2}{3}$π+$\frac{4}{3}$ | D. | $\frac{2}{3}$π+4 |
18.设a=60.7,b=log70.6,c=log0.60.7,则( )
| A. | c>b>a | B. | b>c>a | C. | c>a>b | D. | a>c>b |
15.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点F,作圆x2+y2=$\frac{{a}^{2}}{4}$的一条切线,切点为E,延长FE与双曲线的右支交于点P,若E是线段FP的中点,则该双曲线的离心率为( )
| A. | $\frac{\sqrt{10}}{2}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\sqrt{10}$ | D. | $\sqrt{2}$ |
 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点($\frac{\sqrt{5}}{2}$,$\frac{\sqrt{3}}{2}$),离心率为$\frac{2\sqrt{5}}{5}$,点O位坐标原点.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点($\frac{\sqrt{5}}{2}$,$\frac{\sqrt{3}}{2}$),离心率为$\frac{2\sqrt{5}}{5}$,点O位坐标原点.