题目内容
8.已知函数$f(x)=\frac{3x}{2x+3}$,数列{an}满足a1=1,an+1=f(an),n∈N*,(1)求a2,a3,a4的值;
(2)求证:数列$\left\{{\frac{1}{a_n}}\right\}$是等差数列;
(3)设数列{bn}满足bn=an-1•an(n≥2),b1=3,Sn=b1+b2+…+bn,若${S_n}<\frac{m-2015}{2}$对一切n∈N*成立,求最小正整数m的值.
分析 (1)a1=1,an+1=f(an)=$\frac{3{a}_{n}}{2{a}_{n}+3}$,代值计算即可,
(2)由$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=$\frac{2}{3}$,利用等差数列的通项公式即可得出.
(3)bn=$\frac{9}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),利用“裂项求和”可得Sn,再利用向数列的单调性即可得出.
解答 解:(1)a1=1,an+1=f(an)=$\frac{3{a}_{n}}{2{a}_{n}+3}$,
∴a2=$\frac{3×1}{2×1+3}$=$\frac{3}{5}$,a3=$\frac{3×\frac{3}{5}}{2×\frac{3}{5}+3}$=$\frac{3}{7}$,a4=$\frac{3×\frac{3}{7}}{2×\frac{3}{7}+3}$=$\frac{3}{9}$=$\frac{1}{3}$,
(2)证明:由an+1=f(an)=$\frac{3{a}_{n}}{2{a}_{n}+3}$,
得$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=$\frac{2}{3}$,
∴$\left\{{\frac{1}{a_n}}\right\}$是以首项为1,公差为$\frac{2}{3}$的等差数列;
(3)由(2)可知$\frac{1}{{a}_{n}}$=1+$\frac{2}{3}$(n-1)=$\frac{2}{3}$n+$\frac{1}{3}$=$\frac{1}{3}$(2n+1)
∴an=$\frac{3}{2n+1}$,
当n≥2时,bn=an-1•an=$\frac{9}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),
当n=1时,上式同样成立,
∴Sn=b1+b2+…+bn=$\frac{9}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)=$\frac{9}{2}$(1-$\frac{1}{2n+1}$)≤$\frac{9}{2}$,
∵${S_n}<\frac{m-2015}{2}$对一切n∈N*成立,
∴$\frac{9}{2}$≤$\frac{m-2015}{2}$,
∴m≥2024,
∴最小正整数m的值为2024.
点评 本题考查了等差数列通项公式、“裂项求和”、数列的单调性,考查了推理能力与计算能力,属于中档题.


| A. | 26 | B. | 57 | C. | 120 | D. | 247 |
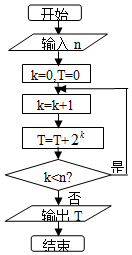
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
| A. | {2,0,1,7} | B. | {0,6,7,8} | C. | {2,3,4,5} | D. | {3,4,5,6} |
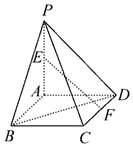 如图,平面PAD⊥平面ABCD,四边形ABCD为正方形,∠PAD=90°,且PA=AD=2,E,F分别是线段PA,CD的中点,则异面直线EF与BD所成角的余弦值为$\frac{\sqrt{3}}{6}$.
如图,平面PAD⊥平面ABCD,四边形ABCD为正方形,∠PAD=90°,且PA=AD=2,E,F分别是线段PA,CD的中点,则异面直线EF与BD所成角的余弦值为$\frac{\sqrt{3}}{6}$.