题目内容
 已知{an}是公差不为0的等差数列,a1=3,现将数列{an}的各项依次放入如图表格中,其中第1行1项,第2行2项,…,第n行2n-1项,记第n行各项的和为Tn,且T1,T2,T3成等比数列.数列{an}的通项公式是( )
已知{an}是公差不为0的等差数列,a1=3,现将数列{an}的各项依次放入如图表格中,其中第1行1项,第2行2项,…,第n行2n-1项,记第n行各项的和为Tn,且T1,T2,T3成等比数列.数列{an}的通项公式是( )| A、an=2n+1 |
| B、an=3n |
| C、an=4n-1 |
| D、an=2n-1 |
考点:等比数列的性质
专题:计算题,等差数列与等比数列
分析:设数列{an}的公差为d,依题意:(a2+a3)2=a1(a4+a5+a6+a7),求出公差,即可求出数列{an}的通项公式.
解答:
解:设数列{an}的公差为d,依题意:(a2+a3)2=a1(a4+a5+a6+a7)
所以(3d+6)2=3(12+18d)⇒d2+4d+4=4+6d⇒d2=2d,
因为d≠0,所以d=2,
因此:an=2n+1.
故选:A.
所以(3d+6)2=3(12+18d)⇒d2+4d+4=4+6d⇒d2=2d,
因为d≠0,所以d=2,
因此:an=2n+1.
故选:A.
点评:本题考查数列{an}的通项公式,考查学生的计算能力,确定数列的公差是关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
若点P(a,b)与Q(b-1,a+1)(a≠b-1)关于直线l对称,则直线l的方程是( )
| A、x+y=0 |
| B、x-y=0 |
| C、x+y-1=0 |
| D、x-y+1=0 |
执行如图所示的程序框图,若m=4,则输出的结果为( )
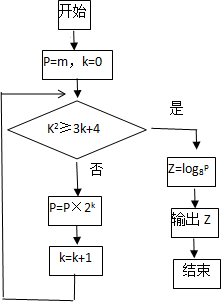

| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
 一个四面体的顶点都在球面上,它们的正视图、侧视图、俯视图都是右图.图中圆内有一个以圆心为中心边长为1的正方形.则这个四面体的外接球的表面积是( )
一个四面体的顶点都在球面上,它们的正视图、侧视图、俯视图都是右图.图中圆内有一个以圆心为中心边长为1的正方形.则这个四面体的外接球的表面积是( ) 如图,有边长为1的正方形,取其对角线的一半,构成新的正方形,再取新正方形的对角线的一半,构成正方形…如此形成一个边长不断缩小的正方形系列.
如图,有边长为1的正方形,取其对角线的一半,构成新的正方形,再取新正方形的对角线的一半,构成正方形…如此形成一个边长不断缩小的正方形系列.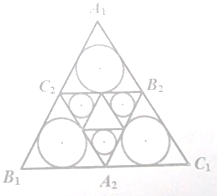 设正三角形A1B1C1边长为a,分别取B1C1,C1A1,A1B1的中点A2,B2,C2,记a1是正三角形A1B1C1除去△A2B2C2后剩下的三个内切圆面积之和,依此类推:记an是△AnBnCn除去△An+1Bn+1Cn+1后剩下的三个三角形内切圆面积之和,从而得到数列{an},设这个数列{an}的前n项和Sn.
设正三角形A1B1C1边长为a,分别取B1C1,C1A1,A1B1的中点A2,B2,C2,记a1是正三角形A1B1C1除去△A2B2C2后剩下的三个内切圆面积之和,依此类推:记an是△AnBnCn除去△An+1Bn+1Cn+1后剩下的三个三角形内切圆面积之和,从而得到数列{an},设这个数列{an}的前n项和Sn.