题目内容
4.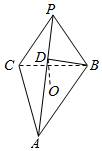 三棱锥P-ABC,底面是边长为2的正三角形,平面PBC⊥平面ABC,PB=PC=2,D为PA上一点,AD=2DP,O为底面三角形中心.
三棱锥P-ABC,底面是边长为2的正三角形,平面PBC⊥平面ABC,PB=PC=2,D为PA上一点,AD=2DP,O为底面三角形中心.(1)求证:DO∥平面PBC;
(2)求证:BD⊥AC.
分析 (1)连接AO交BC于点E,连接PE,由三角形中心的性质可得AO=2OE,从而DO∥PE,得出线面平行;
(2)由平面PBC⊥平面ABC可得PE⊥平面ABC,由DO∥PE可得DO⊥平面ABC,故DO⊥AC,由三角形中心性质得AC⊥BO,从而AC⊥平面DOB,得出BD⊥AC.
解答  解:(1)连接AO交BC于点E,连接PE,
解:(1)连接AO交BC于点E,连接PE,
∵O为正三角形ABC的中心,∴AO=2EO,
又AD=2DP,∴DO∥PE,
∵DO?平面PBC,PE?平面PBC,
∴DO∥平面PBC.
(2)∵PB=PC,且E为BC中点,∴PE⊥BC,
又平面PBC⊥平面ABC,∴PE⊥平面ABC,
由(1)知,DO∥PE,∴DO⊥平面ABC,
∴DO⊥AC.连接BO,则AC⊥BO,
又DO∩BO=O,DO?平面DOB,BO?平面DOB,
∴AC⊥平面DOB,∵BD?平面DOB,
∴AC⊥BD.
点评 本题考查了线面平行,线面垂直的判定,面面垂直的性质,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.设m、n是两条不同的直线,α、β是两个不同的平面,则( )
| A. | 若m∥α,n∥α,则m∥n | B. | 若m∥α,m∥β,则α∥β | C. | 若m∥n,n⊥α,则m⊥α | D. | 若m∥α,α⊥β,则m⊥β |
 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,且BA⊥AC,AC=4,AB=3,二面角B-A1C1-B1的余弦值为$\frac{3}{5}$,E在线段CC1上运动(含端点),F在线段AB上运动(含端点).
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,且BA⊥AC,AC=4,AB=3,二面角B-A1C1-B1的余弦值为$\frac{3}{5}$,E在线段CC1上运动(含端点),F在线段AB上运动(含端点).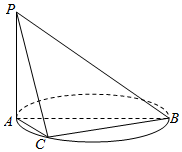 如图,AB时圆O的直径,PA垂直圆所在的平面,C是圆上异于A、B的动点,PA=AB,∠ABC大小为θ,点D、E分别在棱PB,PC上.
如图,AB时圆O的直径,PA垂直圆所在的平面,C是圆上异于A、B的动点,PA=AB,∠ABC大小为θ,点D、E分别在棱PB,PC上.