题目内容

3．已知圆的方程为x2+y2-6x=0，过点（1，2）的该圆的所有弦中，最短弦的长为（　　）
A．$\frac{1}{2}$B．1C．2D．4

分析 化圆的一般方程为标准方程，求出圆心坐标与半径，如何利用垂径定理求得答案．

解答 解：由x2+y2-6x=0，得（x-3）2+y2=9，∴圆心坐标为（3，0），半径为3．
如图：当过点P（1，2）的直线与连接P与圆心的直线垂直时，弦AB最短，

则最短弦长为$2\sqrt{9-[（3-1）^{2}+（0-2）^{2}]}=2$．
故选：C．

点评 本题考查直线与圆的位置关系，考查垂径定理的应用，是基础题．

练习册系列答案
相关题目
13．方程lgx+x-3=0一定有解的区间是（　　）
A．（2，3）B．（1，2）C．（0，1）D．（3，4）
14．已知点P（x，y）在椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$上运动，设$d=\sqrt{{x^2}+{y^2}+4y+4}-\frac{x}{2}$，则d的最小值为（　　）
A．$\sqrt{5}-2$B．$2\sqrt{2}-1$C．$\sqrt{5}-1$D．$\sqrt{6}-1$
11．在数列{an}中，a1=3，a17=67，通项公式是关于n的一次函数．
（1）求数列{an}的通项公式；
（2）求a2013；
（3）2015是否为数列{an}中的项？若是，为第几项？
18．已知幂函数$y={x}^{{p}^{2}-2p-3}$（p∈N*）的图象关于y轴对称，且在（0，+∞）上是减函数，实数a满足$（{a}^{2}-1）^{\frac{p}{3}}＜（3a+3）^{\frac{p}{3}}$，则a的取值范围是（1，4）．
8．已知集合$A=\{x|\frac{x+3}{x-3}≤0\}$，B={x|x-1≥0}，则A∩B为（　　）
A．[1，3]B．[1，3）C．[-3，∞）D．（-3，3]
15．将函数$y=2sin（2x+\frac{π}{6}）$的图象向右平移$\frac{1}{4}$个周期后，所得图象对应的函数为f（x），则函数f（x）的单
调递增区间（　　）
A．$[kπ-\frac{π}{12}，kπ+\frac{5π}{12}]（k∈Z）$B．$[kπ+\frac{5π}{12}，kπ+\frac{11π}{12}]（k∈Z）$
C．$[kπ-\frac{5π}{24}，kπ+\frac{7π}{24}]（k∈Z）$D．$[kπ+\frac{7π}{24}，kπ+\frac{19π}{24}]（k∈Z）$
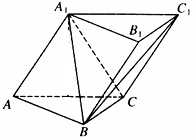12．如图，三棱柱ABC-A1B1C1中，侧面AA1C1C⊥底面ABC，AA1=A1C=AC=2，AB=BC且AB⊥BC，
（Ⅰ）求证：AC⊥A1B；
（Ⅱ）求二面角A-A1C-B的余弦值．
13．设i为虚数单位，复数$\overline{i（1+i）}$的虚部为（　　）
A．-1B．1C．-iD．i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网