题目内容
7.函数y=-x2+2x的图象向左平行移动4个单位,向上平行移动1个单位,所得图象对应的函数解析式是y=-x2-6x-7.分析 先将函数图象向左平移四个单位得到:y=-x2-6x-8,再将得到的函数图象向上平移1个单位得到:y=(-x2-6x-8)+1,进而得到结果.
解答 解:将函数y=-x2+2x的图象向左平移4个单位得到:
y=-(x+4)2+2(x+4)=-x2-6x-8,
再将该函数的图象向上平移1个单位得,
y=(-x2-6x-8)+1=-x2-6x-7,
即所得函数图象对应的解析式为:y=-x2-6x-7,
故答案为:y=-x2-6x-7.
点评 本题主要考查了函数的图象及其变换,涉及函数图象左右平移与上下平移时函数解析式的变化规律,体现了数形结合的解题思想,属于基础题.

练习册系列答案
相关题目
7.已知集合M={(x,y)|x2+y2≤1},若实数λ,μ满足:对任意的(x,y)∈M,都有(λx,μy)∈M,则称(λ,μ)是集合M的“和谐实数对”.则以下集合中,存在“和谐实数对”的是( )
| A. | {(λ,μ)|λ+μ=4} | B. | {(λ,μ)|λ2+μ2=4} | C. | {(λ,μ)|λ2-4μ=4} | D. | {(λ,μ)|λ2-μ2=4} |
2.已知a=1.7-2.5,b=2.51.7,c=${log_2}{\frac{2}{3}}$,则a,b,c的大小关系为( )
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | c<a<b |
12.(1)若不等式$sin(2x+\frac{π}{3})-\frac{1}{a}>0$对$x∈[\frac{π}{6},\frac{π}{2}]$的所有实数x都成立,求a的取值范围;
(2)若不等式x2-2ax+2a+1>0对0≤x≤1的所有实数x都成立,求a的取值范围;
(3)设a>0且a≠1,f(x)=x2-ax,对x∈(-1,1),均有$f(x)<\frac{1}{2}$,求a的范围.
(4)完成填空
(2)若不等式x2-2ax+2a+1>0对0≤x≤1的所有实数x都成立,求a的取值范围;
(3)设a>0且a≠1,f(x)=x2-ax,对x∈(-1,1),均有$f(x)<\frac{1}{2}$,求a的范围.
(4)完成填空
| 用图象语言表述 | 用函数最值表述 | |
| 在(a,b)内,若对任意的x有f(x)>g(x)成立 | ① | ② |
| 在(a,b)内,若存在x0,使f(x)>g(x)成立 | ③ | ④ |
17.${(x-\frac{2}{x^2})^6}$展开式中的常数项为( )
| A. | 60 | B. | -60 | C. | 30 | D. | -30 |
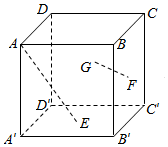 在正方体ABCD-A′B′C′D′中,E,F,G分别是面A′C′,面B′C,面CD′的中心,则AE与FG所成的角大小为多少?
在正方体ABCD-A′B′C′D′中,E,F,G分别是面A′C′,面B′C,面CD′的中心,则AE与FG所成的角大小为多少?