题目内容
10.若实数x,y满足$\left\{\begin{array}{l}{x+y≥0}\\{x≤1}\\{x-2y≥0}\end{array}\right.$,则x的取值范围是[0,1],|x|+|y|的取值范围是[0,2].分析 由约束条件作出可行域,得到x的范围,分类去绝对值得到z=|x|+|y|,求得不同情况下的最值,取并集得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{x+y≥0}\\{x≤1}\\{x-2y≥0}\end{array}\right.$作出可行域如图,
由图可知,0≤x≤1;
当x≥0,y≥0时,z=|x|+|y|=x+y过(1,$\frac{1}{2}$)时有最大值为$\frac{3}{2}$,过O(0,0)时有最小值0;
当x≥0,y≤0时,z=|x|+|y|=x-y过(1,-1)时有最大值为2,过O(0,0)时有最小值0.
∴|x|+|y|的取值范围是[0,2].
故答案为:[0,1],[0,2].
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
1.对于实数x,符号[x]表示不超过x的最大整数,例如[π]=3,[-1.08]=-2,如果定义函数f(x)=x-[x],那么下列命题中正确的序号有( )
①f(x)的定义域为R,值域为[0,1]②f(x)在区间[0,1)上单调递增
③f(x)既不是奇函数也不是偶函数 ④函数f(x)与g(x)=log5(-x)图象有5个交点.
①f(x)的定义域为R,值域为[0,1]②f(x)在区间[0,1)上单调递增
③f(x)既不是奇函数也不是偶函数 ④函数f(x)与g(x)=log5(-x)图象有5个交点.
| A. | ①②③ | B. | ②③ | C. | ①②③④ | D. | ②③④ |
18.设i是虚数单位,若复数z满足(2-5i)z=29,则z=( )
| A. | 2-5i | B. | 2+5i | C. | -2-5i | D. | -2+5i |
15.“a=5”是“点(2,1)到直线x=a的距离为3”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
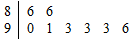 如图是某班8位学生诗词比赛得分的茎叶图,那么这8位学生得分的众数和中位数分别为93、92.
如图是某班8位学生诗词比赛得分的茎叶图,那么这8位学生得分的众数和中位数分别为93、92.