题目内容
5.在ABC中,角A,B,C的对边分别为a,b,c,若cosA=$\frac{4}{5}$,B=$\frac{π}{3}$,a=3,则b=$\frac{5\sqrt{3}}{2}$.分析 由已知利用同角三角函数基本关系式可求sinA,进而利用正弦定理即可得解.
解答 解:∵cosA=$\frac{4}{5}$,
∴sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{3}{5}$,
∵由正弦定理得$\frac{a}{sinA}=\frac{b}{sinB}$,即$\frac{3}{\frac{3}{5}}=\frac{b}{\frac{\sqrt{3}}{2}}$,
∴b=$\frac{5\sqrt{3}}{2}$.
故答案为:$\frac{5\sqrt{3}}{2}$.
点评 本题主要考查了同角三角函数基本关系式,正弦定理在解三角形中的应用,属于基础题.

练习册系列答案
相关题目
15.由0,1,2,3,5组成的无重复数字的五位偶数共有( )
| A. | 36个 | B. | 42个 | C. | 48个 | D. | 120个 |
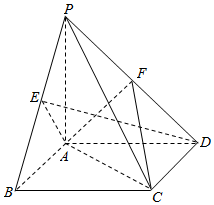 在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,E,F分别是PB,PD的中点.
在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,E,F分别是PB,PD的中点.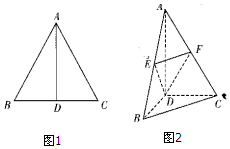 如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.
如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.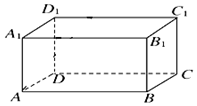 如图,长方体ABCD-A1B1C1D1中,AB=20,BC=13,AA1=12,过点A1D1的平面α与棱AB和CD分别交于点E、F,四边形A1EFD1为正方形.
如图,长方体ABCD-A1B1C1D1中,AB=20,BC=13,AA1=12,过点A1D1的平面α与棱AB和CD分别交于点E、F,四边形A1EFD1为正方形.