题目内容
8.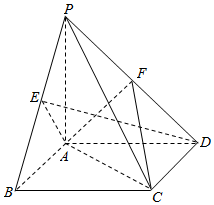 在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,E,F分别是PB,PD的中点.
在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,E,F分别是PB,PD的中点.(Ⅰ)求证:PB∥平面FAC;
(Ⅱ)求三棱锥P-EAD的体积;
(Ⅲ)求证:平面EAD⊥平面FAC.
分析 (Ⅰ)连接BD,与AC交于点O,连接OF,推导出OF∥PB,由此能证明PB∥平面FAC.
(Ⅱ)由PA⊥平面ABCD,知PA为棱锥P-ABD的高.由S△PAE=S△ABE,知${V_{P-EAD}}=\frac{1}{2}×{V_{P-ABD}}$,由此能求出结果.
(Ⅲ)推导出AD⊥PB,AE⊥PB,从而PB⊥平面EAD,进而OF⊥平面EAD,由此能证明平面EAD⊥平面FAC.
解答  证明:(Ⅰ)连接BD,与AC交于点O,连接OF,
证明:(Ⅰ)连接BD,与AC交于点O,连接OF,
在△PBD中,O,F分别是BD,PD的中点,
所以OF∥PB,
又因为OF?平面FAC,PB?平面FAC,
所以PB∥平面FAC.
解:(Ⅱ)因为PA⊥平面ABCD,所以PA为棱锥P-ABD的高.
因为PA=AB=2,底面ABCD是正方形,
所以${V_{P-ABD}}=\frac{1}{3}×{S_{△ABD}}×PA$=$\frac{1}{3}×\frac{1}{2}×2×2×2=\frac{4}{3}$,
因为E为PB中点,所以S△PAE=S△ABE,
所以${V_{P-EAD}}=\frac{1}{2}×{V_{P-ABD}}=\frac{2}{3}$.
证明:(Ⅲ)因为AD⊥平面PAB,PB?平面PAB,
所以AD⊥PB,
在等腰直角△PAB中,AE⊥PB,
又AE∩AD=A,AE?平面EAD,AD?平面EAD,
所以PB⊥平面EAD,
又OF∥PB,
所以OF⊥平面EAD,
又OF?平面FAC,
所以平面EAD⊥平面FAC.
点评 本题考查线面平行、面面垂直的证明,考查三棱锥的体积的求法,考查推理论证能力、空间思维能力、运算求解能力,考查转化化归思想、数形结合思想,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.对函数f(x)=$\frac{cosx+m}{cosx+2}$,若?a,b,c∈R,f(a),f(b),f(c)都为某个三角形的三边长,则实数m的取值范围是( )
| A. | $(\;\frac{5}{4}\;,\;6\;)$ | B. | $(\;\frac{5}{3}\;,\;6\;)$ | C. | $(\;\frac{7}{5}\;,\;5\;)$ | D. | $(\;\frac{5}{4}\;,\;5\;)$ |
16.圆心为(0,1)且与直线y=2相切的圆的方程为( )
| A. | (x-1)2+y2=1 | B. | (x+1)2+y2=1 | C. | x2+(y-1)2=1 | D. | x2+(y+1)2=1 |
7.设m∈R,命题:若m>0,则x2+x-m=0有实根的否命题是( )
| A. | 若m>0,则x2+x-m=0没有实根 | B. | 若m<0,则x2+x-m=0没有实根 | ||
| C. | 若m≤0,则x2+x-m=0有实根 | D. | 若m≤0,则x2+x-m=0没有实根 |