题目内容
14.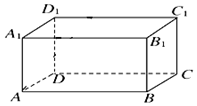 如图,长方体ABCD-A1B1C1D1中,AB=20,BC=13,AA1=12,过点A1D1的平面α与棱AB和CD分别交于点E、F,四边形A1EFD1为正方形.
如图,长方体ABCD-A1B1C1D1中,AB=20,BC=13,AA1=12,过点A1D1的平面α与棱AB和CD分别交于点E、F,四边形A1EFD1为正方形.(1)在图中请画出这个正方形(注意虚实线,不必写作法),并求AE的长;
(2)问平面α右侧部分是什么几何体,并求其体积.
分析 (1)由长方体的结构特征能求出交线围成的正方形A1EFD1,在Rt△A1AE中,由勾股定理能求出AE的长.
(2)平面α右侧部分的几何体是以A1EBB1和为底面的直四棱柱,由棱柱体积公式得该直四棱柱的体积.
解答 解:(1)交线围成的正方形A1EFD1如图所示(不分实虚线的酌情给分)… (3分)
(3分)
∵A1D1=A1E=13,A1A=12,
在Rt△A1AE中,
由勾股定理知AE=$\sqrt{{A}_{1}{E}^{2}-A{{A}_{1}}^{2}}$=5.…(6分)
(2)平面α右侧部分的几何体是以A1EBB1和为底面的直四棱柱,(棱柱或四棱柱均不扣分)
由棱柱体积公式得该直四棱柱的体积:
V=${S}_{梯形{A}_{1}EB{B}_{1}}×BC$=$\frac{1}{2}×(20+15)×12$×13=2730.
(由体积之差法也不扣分)….(12分)
点评 本题考查满足条件的正方形的作法,考查线段长的求法,考查几何体的体积的求法,考查推理论证能力、运算求解能力、空间思维能力,考查转化化归思想、数形结合思想,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.已知函数f(x)是偶函数,定义域为R,g(x)=f(x)+2x,若g(log27)=3,则$g({{{log}_2}\frac{1}{7}})$=( )
| A. | -4 | B. | 4 | C. | $-\frac{27}{7}$ | D. | $\frac{27}{7}$ |
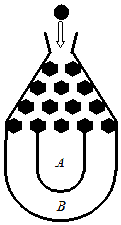 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.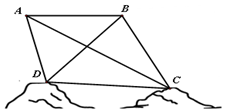 为绘制海底地貌图,测量海底两点C,D间的距离,海底探测仪沿水平方向在A,B两点进行测量,A,B,C,D在同一个铅垂平面内.海底探测仪测得∠BAC=30°,∠DAC=45°,∠ABD=45°,∠DBC=75°,同时测得$AB=\sqrt{3}$海里.
为绘制海底地貌图,测量海底两点C,D间的距离,海底探测仪沿水平方向在A,B两点进行测量,A,B,C,D在同一个铅垂平面内.海底探测仪测得∠BAC=30°,∠DAC=45°,∠ABD=45°,∠DBC=75°,同时测得$AB=\sqrt{3}$海里.