题目内容
8.已知函数f(x)=1g(x+$\sqrt{{x}^{2}+1}$),若对于任意的x∈(1,2]时,f($\frac{x+1}{x-1}$)+f[$\frac{m}{(x-1)^{2}(x-6)}$]>0恒成立,则实数m的取值范围是( )| A. | [4,+∞) | B. | (12,+∞) | C. | (-∞,0) | D. | (-∞,0] |
分析 根据函数的表达式可判断函数为奇函数,且单调递增.不等式可整理为(x+1)(x-1)(x-6)<-m恒成立,只需构造函数h(x)=(x+1)(x-1)(x-6),求出区间内的最大值即可.因为x∈(1,2],故能取等号.
解答 解:∵f(x)=1g(x+$\sqrt{{x}^{2}+1}$),
∴f(-x)=1g(-x+$\sqrt{{x}^{2}+1}$)
=-f(x),
∴函数为奇函数,由表达式显然知函数为增函数,
∵f($\frac{x+1}{x-1}$)+f[$\frac{m}{(x-1)^{2}(x-6)}$]>0恒成立,
∴$\frac{x+1}{x-1}$>-$\frac{m}{(x-1)^{2}(x-6)}$,
∴(x+1)(x-1)(x-6)<-m恒成立,
令h(x)=(x+1)(x-1)(x-6),可知函数h(x)在x∈(1,2]时,单调递减,
∴h(x)的最大值大于h(1)=0,
∴0≤-m,
∴m≤0,
故选:D.
点评 本题考查了函数的奇偶性和单调性和应用,利用构造函数的方法,通过求函数的最值解决恒成立问题.

练习册系列答案
相关题目
19.已知命题:“若abc=0,则实数a,b,c中至少有一个为0”,用反证法证明该命题时的假设为( )
| A. | 假设a,b,c都不为0 | B. | 假设a,b,c中至少有两个为0 | ||
| C. | 假设a,b,c中至多有两个为0 | D. | 假设a,b,c中至多有一个为0 |
16.若关于x的方程3x=$\frac{a+3}{5-a}$无负数根,则a的取值范围为( )
| A. | a≥1 | B. | a<5 | C. | (-∞,1]∪(5,+∞) | D. | [1,5) |
13.相距1400m的A、B两个哨所,听到炮弹爆炸的时间相差3s,已知声速340m/s,则炮弹爆炸点所在曲线的离心率为( )
| A. | $\frac{51}{70}$ | B. | $\frac{70}{51}$ | C. | $\frac{35}{17}$ | D. | 1 |
18.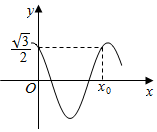 已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=f(0),则正确的选项是( )
已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=f(0),则正确的选项是( )
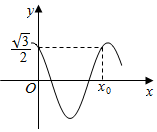 已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=f(0),则正确的选项是( )
已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=f(0),则正确的选项是( )| A. | $φ=\frac{π}{6},{x_0}=\frac{5}{3}$ | B. | $φ=\frac{π}{6},{x_0}=1$ | C. | $φ=\frac{π}{3},{x_0}=\frac{5}{3}$ | D. | $φ=\frac{π}{3},{x_0}=1$ |
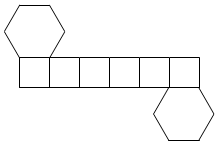 已知一个凸多边形的平面展开图由两个正六边形和六个正方形构成,如图所示,若该凸多面体所有棱长均为1,则其体积V=$\frac{3\sqrt{3}}{2}$.
已知一个凸多边形的平面展开图由两个正六边形和六个正方形构成,如图所示,若该凸多面体所有棱长均为1,则其体积V=$\frac{3\sqrt{3}}{2}$.