题目内容
20.设f(x)为定义在R上的奇函数,若当x>0时,f(x)=3x+1,则f(log3$\frac{1}{2}$)=-6.分析 由奇函数的性质得当x<0时,f(x)=-3-x+1,从而f(log3$\frac{1}{2}$)=-${3}^{-lo{g}_{3}\frac{1}{2}+1}$,由此利用对数性质能求出结果.
解答 解:∵f(x)为定义在R上的奇函数,当x>0时,f(x)=3x+1,
∴当x<0时,f(x)=-3-x+1,
∴f(log3$\frac{1}{2}$)=-${3}^{-lo{g}_{3}\frac{1}{2}+1}$
=-${3}^{lo{g}_{3}2}$×3
=-2×3
=-6.
故答案为:-6.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数奇偶性、对数性质的合理运用.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
8.已知函数f(x)=1g(x+$\sqrt{{x}^{2}+1}$),若对于任意的x∈(1,2]时,f($\frac{x+1}{x-1}$)+f[$\frac{m}{(x-1)^{2}(x-6)}$]>0恒成立,则实数m的取值范围是( )
| A. | [4,+∞) | B. | (12,+∞) | C. | (-∞,0) | D. | (-∞,0] |
12.已知2sin2α=1+cos2α,则tan(α+$\frac{π}{4}$)的值为( )
| A. | -3 | B. | 3 | C. | -3或3 | D. | -1或3 |
9.若非空集合A,B满足A?B,则“x∈A”是“x∈B”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
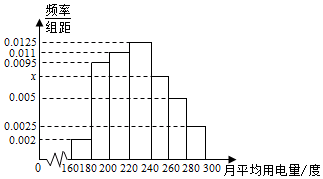 某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.
某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.