题目内容
设F1、F2分别为双曲线C:
-
=1(a,b>0)的左右焦点,A为双曲线的左顶点,以F1F2为直径的圆交双曲线某条渐近线于M、N两点,且满足∠MAN=120°,则该双曲线的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:先求出M,N的坐标,再利用余弦定理,求出a,c之间的关系,即可得出双曲线的离心率.
解答:
解:设以F1F2为直径的圆与渐近线y=
x相交与点M的坐标为(x0,y0)(x0>0),
根据对称性得N点的坐标为(-x0,-y0),
∴
;
解得M(a,b),N(-a,-b);
又∵A(-a,0),且∠MAN=120°,
∴由余弦定理得4c2=(a+a)2+b2+b2-2
•bcos 120°,
化简得7a2=3c2,
∴e=
=
.
故答案为:
.
| b |
| a |
根据对称性得N点的坐标为(-x0,-y0),
∴
|
解得M(a,b),N(-a,-b);
又∵A(-a,0),且∠MAN=120°,
∴由余弦定理得4c2=(a+a)2+b2+b2-2
| (a+a)2+b2 |
化简得7a2=3c2,
∴e=
| c |
| a |
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题考查了双曲线的标准方程与几何性质的应用问题,解题时应熟记它的几何性质是什么,属于基础题.

练习册系列答案
相关题目
已知函数为奇函数,且当x>0时,f(x)=log2(x-1)+x2-a,且f(2)=1,则f(-3)=( )
| A、-1 | B、1 | C、-7 | D、7 |
双曲线x2-y2=a(a≠0)的离心率是( )
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
已知g(x)=1-2x,f[g(x)]=
,则f(-3)等于( )
| 1 |
| 2x+2 |
A、
| ||
B、
| ||
C、
| ||
| D、4 |
若{1,2}⊆A⊆{1,2,3,4,5}}则满足条件的集合A的个数是( )
| A、6 | B、7 | C、8 | D、9 |
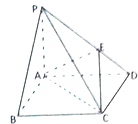 已知四棱锥P-ABCD中,PA=AB,PA⊥底面ABCD,ABCD是平行四边形,且∠BAC=90°.
已知四棱锥P-ABCD中,PA=AB,PA⊥底面ABCD,ABCD是平行四边形,且∠BAC=90°.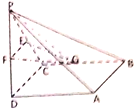 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,如果PD⊥平面ABCD,PD=AB=2,E,F,G分别为PC,PD,BC的中点
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,如果PD⊥平面ABCD,PD=AB=2,E,F,G分别为PC,PD,BC的中点